Other affiliations:
Research Interests (in chronological order). Note that the more recent topics may not be up-to-date. To get a better idea of my recent interests, check my publication list which is kept up-to-date.
The meron-vortex model for high Tc superconductivity:
The occurrence of high Tc
superconductivity in layered perovskite materials has sparked broad
interest in the quantum properties of magnetically correlated electron
systems. At low temperature all parent compounds (such as LaCuO or
YBaCuO, see figures 1 and 2) are insulators with long-range
antiferromagnetic order in the CuO planes. As charge carriers are
introduced in the CuO planes by doping, this long range AFM order
disappears, leading to a metallic phase with striking non-Fermi-liquid
properties. Superconductivity emerges from this unconventional metal
as the system is cooled. The development of a microscopic model of
this unconventional metal is one of the outstanding issues in quantum
many-body theory.
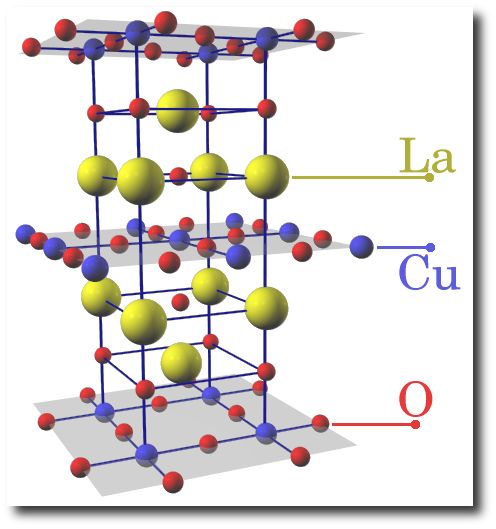
Fig. 1: LaCuO parent compound |
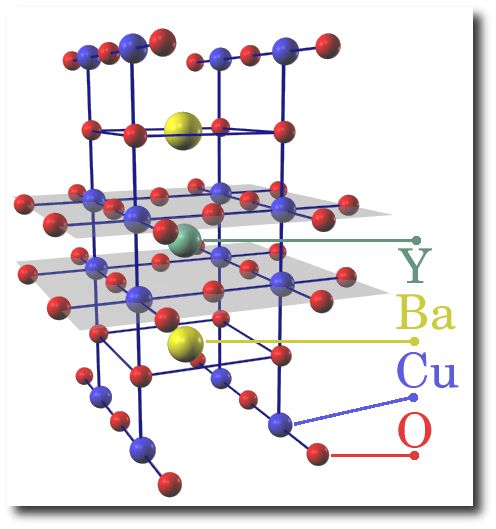
Fig. 2: YBaCuO parent
compound |
I have a long-standing interest in this problem, which started with my
Ph.D. work with Prof. Sajeev John from
University of Toronto. He proposed a new microscopic model (the
spin-flux Hamiltonian) for a strongly repulsive electron gas on a 2D
square lattice. The rough idea is that nearest neighbor Coulomb
repulsion stabilizes a state in which electrons undergo a "somersault"
in their internal spin-space (spin-flux). We have shown that when this
spin-1/2 antiferromagnetic (AFM) insulator is doped, the charge
carriers nucleate mobile, charged, bosonic vortex solitons accompanied
by unoccupied states deep inside the Mott-Hubbard charge-transfer gap.
Our model provides a unified microscopic basis for (i)
non-Fermi-liquid transport properties, (ii) mid-infrared optical
absorption, (iii) destruction of AFM long range order with doping,
(iv) angled resolved spectroscopy (ARPES), and (v) d-wave preformed
charged carrier pairs. The approximation used to study the 2D
spin-flux Hubbard model is the Configuration Interaction Method. In
1D, this approximation leads to excellent agreement with the exact
Bethe Ansatz results, as well as a clear demonstration of the
spin-charge separation: the charge is carried by charged bosonic
domain-walls, while the spin is carried by neutral fermionic
domain-walls.
Details are presented in this on-line
presentation as well as in this
review article. You can also look
at this
more recent poster or
this
older poster. Future work will
concentrate on investigations of various magnetic, transport and
optical properties of this model, so that a detailed comparison with
available experiments can be carried out.
Publications
- Midgap states of a two-dimensional antiferromagnetic Mott insulator:
Electronic structure of meron-vortices Sajeev John, Mona Berciu and Andrey Golubentsev, Europhys. Lett.
41, pp. 31-36 (1998).
- Charged bosons in a doped Mott insulator: Electronic properties of domain
wall solitons and meron vortices Mona Berciu and Sajeev John, Phys. Rev. B 57, pp. 9521-9543 (1998).
- Numerical study of multisoliton configurations in a doped antiferromagnetic
Mott insulator Mona Berciu and Sajeev John, Phys. Rev. B 59, pp. 15143-15159 (1999).
- Quantum dynamics of charged and neutral magnetic solitons: Spin-charge separation in
the one-dimensional Hubbard model Mona Berciu and Sajeev John, Phys. Rev. B 61, pp. 10015-10028 (2000).
- Microscopic model for d-wave charge-carrier pairing and non-Fermi-liquid behavior
in a purely repulsive two-dimensional electron system Mona Berciu and Sajeev John, Phys. Rev. B 61, pp. 16454-16469 (2000).
- Microscopic model for d-wave pairing in cuprates: what happens when electrons somersault?
Mona Berciu and Sajeev John, Physica B 296, pp. 143-155 (2001).
- Magnetic structure factor in cuprate superconductors: the meron-vortex model, Mona Berciu and Sajeev John, Phys. Rev. B 69, 224515 (2004).
go to top
Diluted magnetic semiconductors:
Diluted magnetic semiconductors (DMS) are semiconductors of the
general type (A,Mn)B, where AB is either a II-VI or a III-V
semiconductor and M a magnetic element, most commonly Mn. Substitution
of a small fraction x of the element A by Mn impurities (and in the
case of II-VI semiconductors an additional charge dopant, such as valence-V P on
the B site) leads to the emergence of a semiconductor with
ferromagnetic properties. This is due to the
interactions of the S=5/2 Mn spins (coming from the
half-filled 3d shell of the Mn) with the spins of the charge carriers
introduced by the Mn dopants, or, in the case of II-VI semiconductors,
by the additional dopant.
Thus, DMS cane be thought of as an inert host
semiconductor doped with both localized spins and
carriers (electrons or holes) that are either itinerant, or localized
on a much longer length scale. In that sense, they belong to the
general family of correlated electron systems, which include a number
of fascinating materials such as cuprates, manganites, heavy fermions
and other Kondo lattice systems.
Electronic materials containing local moments have been studied for
a long time. What makes the DMS so fascinating is that they belong to a
regime that has previously been neglected. While the name diluted
magnetic semiconductors implies (correctly) that the system has only a
small percentage of localized spins, they are at the opposite extreme
of the dilute magnetic alloys such as Fe or Mn in Cu, the canonical
systems involving itinerant fermion and localized spin degrees of
freedom, which have been studied extensively. In the
dilute magnetic metallic alloys, the low density of spins are a
perturbation on the Fermi liquid representing the non-magnetic host
metal. As a result, depending on the concentration of the local moments, they
may be studied in terms of dilute Kondo systems, or amorphous magnetic
systems with a spin-spin coupling mediated by the Fermi sea of
conduction electrons (RKKY coupling), which lead often to spin glass
behavior.
By contrast, in the regime of interest, the carrier density in DMS is
significantly lower than the (low) localized moment density, so
the spins become an integral part of the description of the system and
its magnetic phase, rather than a mere perturbation on a metallic
Fermi sea. In that sense, the situation is even more extreme than
e.g., in Kondo lattice and heavy Fermion materials, where the two
species have comparable densities. This large, inverted, ratio of
local moments to carriers is in fact similar to that in the high Tc
cuprates. However, unlike the cuprates, the density of local moments
is low and incommensurate with the lattice, and the carriers and the
spins are not in the same band. As a consequence of the low moment
density, the exchange between local moments is not standard direct or
superexchange, as in the cuprates, but is mediated by the carriers,
even though their density is so small. Thus, the DMS are in rather
different region of phase space of electronic materials with local
moments, than other correlated electron systems.
Despite this difference, most models of diluted magnetic
semiconductors start from the high carrier density limit, where the
carriers may be modeled as free carriers moving in the conduction or
valence band. This is understandable, since in
the high density limit the carrier kinetic energy is the largest
energy in the problem, and calculations may be done perturbatively
starting from the non-interacting Fermi gas. However, most of the
interesting behavior is seen at low carrier densities, where the
system is insulating, or not too far from the metal-insulator
transition. Consequently, in collaboration with Prof. R. N. Bhatt
from Princeton University, we have concentrated on the
low density regime, investigating a simple model describing
carriers in an impurity band formed from the bound impurity states.
We found that disorder in the position of Mn atoms has significant influence on the
properties of the system; for instance, increased disorder leads to a higher critical temperature.
Here is a recent poster on this work.
We have performed mean-field and Monte Carlo investigations of this Hamiltonian, as well as used random-phase
approximation to compute the corresponding spin-wave spectra. Future work will concentrate on computation of
various response functions, as well as on the possible use of such materials for devices.
Publications
Effects of disorder on ferromagnetism in diluted magnetic semiconductors
Mona Berciu and R.N. Bhatt, Phys. Rev. Lett. 87, 107203 (2001).
Two-component approach for thermodynamic properties in diluted magnetic semiconductors
Malcolm P. Kennett, Mona Berciu and R.N. Bhatt, Phys. Rev. B 65, 115308 (2002).
Mean-Field Approach to Disorder Effects on Ferromagnetism in GaMnAs
Mona Berciu and R. N. Bhatt, Physica B 312-313 , pp. 815-817 (2002).
Numerical simulations of random spins (and fermionic) models with a wide distribution of energy scales
R. N. Bhatt, Xin Wan, Malcolm P. Kennett and Mona Berciu, Comp. Phys. Comm. 147, 684-689 (2002).
Monte Carlo simulations of an impurity-band model for III-V diluted magnetic semiconductors
Malcolm P. Kennett, Mona Berciu and R.N. Bhatt, Phys. Rev. B 66, 045207 (2002).
Diluted Magnetic Semiconductors in the Low Carrier Density Regime"
R. N. Bhatt, Mona Berciu, Malcolm P. Kennett and Xin Wan, J. of Supercond.: INM 15 , pp. 71-83 (2002).
Spin-waves in disordered III-V diluted magnetic semiconductors
Mona Berciu and R.N. Bhatt, Phys. Rev. B 66, 085207 (2002).
Mean-field approach to disorder effects on ferromagnetism in (III,Mn)V at low carrier densities,
Mona Berciu and R. N. Bhatt, Phys. Rev. B 69, 045202 (2004).
Magnetic susceptibility of diluted magnetic semiconductors at low carrier densities, Adel Kassaian and Mona Berciu, Phys. Rev. B 71, 125203 (2005).
go to top
Photonic band-gap materials:
Photonic crystals are the optical analog of electronic crystals: the dispersion relations for photons have
bands of allowed photonic states separated by gaps in which light cannot propagate. Various photonic crystal
structures are known
to have full, 3D gaps. However, some of the proposed structures are extremely hard to realize experimentally. Thus,
there is a significant effort to find optimized structures, which have large gaps, and which can also be easily
created experimentally. My interests in this field are also related
to investigating the role of the symmetries of the photonic lattice on the properties of its dispersion bands and
those of various defects that can be introduced in such crystals. I am also very interested in studying the role
of disorder on the density of photonic states.
- Photonic band gaps based on tetragonal lattices of slanted pores, Ovidiu Toader, Mona Berciu and Sajeev John, Phys. Rev. Lett. 90, 233901 (2003).
go to top
Integer Quantum Hall Effect:
My interest in this field has started with a collaboration with experimentalists from Princeton University, who were hoping to measure the Hofstadter butterfly in a 2DES modulated with a triangular periodic gate, with a lattice constant of around 39nm. The butterly cannot be observed directly, due to the fact that disorder is still significantly larger than the periodic modulation. However, the small periodic potential has a significant effect on the nature of the electron wavefunctions, particularly close to the critical regime (see pictures below for some local densities of states projected onto the lowest Landau level, without (a) and with (b) a periodic modulation; (d) shows the semi-classical prediction). This results in a reproducible fluctuation-like pattern in the longitudinal conductivity, which was indeed measured experimentally.
After some work, in collaboration primarily with Chenggang Zhou, to try to understand these effects, we then studied fluctuations of the longitudinal and Hall resistivities of mesoscopic samples, close to the transition between integer Quantum Hall plateaus. We performed first-principle simulations to compute these quantities and found excellent agreement with measurements done in D. Shahar's group, at Weismann Institute. We then explained the behaviour observed based on a simple generalization of the Landauer-Buttiker model, which takes into account both tunneling and chiral currents -- the co-existing mechanism for transport.
- A Laterally Modulated 2D Electron System in the Extreme Quantum Limit, Sorin Melinte, Mona Berciu, Chenggang Zhou et. al., Phys. Rev. Lett. 92, 036802 (2004).
- The longitudinal conductance of mesoscopic Hall samples with arbitrary disorder and periodic modulations, Chenggang Zhou and Mona Berciu, Phys. Rev. B 70, 165318 (2004).
- Resistance fluctuations near integer quantum Hall transitions in mesoscopic samples, Chenggang Zhou and Mona Berciu, Europhys. Lett. 69, 602-608 (2005).
- Effects of large disorder on the Hofstadter butterfly, Chenggang Zhou, Mona Berciu and R. N. Bhatt, Phys. Rev. B 71, 125310 (2005).
- Correlated mesoscopic fluctuations in integer quantum Hall transitions, Chenggang Zhou and Mona Berciu, Phys. Rev. B 72, 085306 (2005).
go to top
Spintronic devices:
One of the central features of magnetic semiconductors (both the new III-Mn-V materials and the more established II-Mn-VI) is that a relatively small external magnetic field causes enormous Zeeman splitting. This effect can be used in conjunction
with external inhomogeneous magnetic fields to engineer spin-polarized
charge-carrier eigenstates with certain desirable features. Producing the required nonuniform magnetic fields with nano-scale spatial variation is a formidable problem beyond present nano-lithographic capabilities. We overcome this challenge with hybrid structures that couple the magnetic semiconductor with a superconductor in its vortex phase and/or with nanomagnets of various shapes. The spin-polarized carrier states trapped in the regions of high magnetic field exhibit various interesting properties that can be controlled by controlling the applied magnetic field.
 |
Publications
Nanoscale Zeeman localization of charge carriers in diluted magnetic semiconductor-permalloy hybrids, Mona Berciu and Boldizsar Janko, Phys. Rev. Lett. 90 , 246804 (2004).
Manipulating nanoscale spin and charge textures in diluted magnetic semiconductors using superconducting vortices, M. Berciu, T. Rappoport and B. Janko, Nature 435, 71-75 (2005).
The effect of the Abrikosov vortex phase on spin and charge states in magnetic semiconductor-superconductor hybrids, Tatiana G. Rappoport, Mona Berciu, and Boldizsar Janko, Phys. Rev. B 74, 094502 (2006).
go to top
Polarons and bipolarons
We have developed a novel, highly efficient yet accurate analytical
approximation for the Green's function of a Holstein polaron. It is
obtained by summing all the self-energy diagrams, but with each
self-energy diagram averaged over the momenta of its free
propagators. The result becomes exact for both zero bandwidth and
for zero electron-phonon coupling, and is accurate everywhere in the
parameter space. The resulting Green's function satisfies exactly
the first six spectral weight sum rules. All higher sum rules are
satisfied with great accuracy, becoming asymptotically exact for
coupling both much larger and much smaller than the free particle
bandwidth. Comparison with existing numerical data also confirms
this accuracy. We used this approximation to analyze in detail the
redistribution of the spectral weight as the coupling strength
varies. This method is currently being generalized for more complicated models.
Publications
Green's function of a dressed particle, Mona Berciu, Phys. Rev. Lett. 97, 036402 (2006).
The Green's function of the Holstein polaron, Glen L. Goodvin, Mona Berciu, and George A. Sawatzky, submitted to PRB;
go to top

