...s¹

From now on a small letter (say s₀) denotes a value while a capital letter denotes a random variable.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... rate²

For simplicity you may assume r=0 for now!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... SIZE="+3">NO!!!³

This is a bit of exaggeration, I will discuss this on section .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ⁴

In economics there is a very fancy term for this: short-selling of stock. In real life, one doesn't need to be that sure whether one will have the stock in the future in order to short sell, just that one will be doomed if the stock prices go up!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... free.⁵

Economists call the process of making risk free money arbitrage and the pricing of financial things to prevent arbitrage is called arbitrage free pricing (as opposed to the conventional pricing by probability).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... derivatives⁶

As far as I know, a derivative is something other than stocks and bonds that can be traded. The offer discussed in is what economists call a forward. A forward contract on stock means the buyer of the forward has the obligation to buy the stock a time T (the time the derivative matures) at a predetermined price set at time zero. There is also another kind of derivative called option whereas the buyer of the option has the right, rather than obligation to buy the stock at time T (the time the derivative matures) at the predetermined price set at time zero.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... payout⁷

The payout of a derivative is the amount the buyer of the derivative would get precisely at the time the derivative matures (in the case of figure , the maturity date is time T).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... much⁸

Let me make this straight once and for all, there are at least two kinds of prices related with a derivative: the strike price, k, and the price, p, of the derivative itself. The strike price is the predetermined price set at time zero that the buyer of the derivative can use this price (or should, depending on the type of the derivative concerned) to buy the stock at time T, whereas the price of the derivative is the extra cost (or `entrance fee' if you like) the buyer has to pay in order to enjoy the (potential) benefits (say getting a stock at a lower cost at time T) of the derivative. Referring to the game discussed in game , the strike price k is $s_{0}\exp(rT)$ while the price p of the offer itself is zero! I will discuss this in detail later.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... worth?⁹

From now on, the price of a derivative itself (given a strike price k) means the price at time zero. Of course, the price of that derivative in time T is just f(2) or f(1) depending on whether the stock is going up or down.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

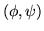...$(\phi,\psi)$¹⁰

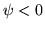$\psi<0$ means one is selling bonds to raise money.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... equations¹¹

The equations and represent the content of the portfolio one has to hold at time zero so that at time T, the values of the stocks and bonds (i.e. one's portfolio) would exactly match the payout of the derivative, no matter what the stock prices are.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... unit¹²

Obviously he can buy an arbitrary number of units of derivatives, using 1 unit is just for simplicity!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... ¹³

If you don't understand, please look at equations and .

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... zero.¹⁴

Normally, one sets k to find p but there is no reason not to do it the other way!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...k¹⁵

The assumption here is that s_down<k<s_up.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...(1)=0¹⁶

That is, the buyer of the option is clever enough not to exercise the option and buy the stock at a higher price than the market price!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

....¹⁷

If you get lost in all those financial terms, let me remind you that this situation is entirely equivalent to the situation that at time zero someone tells you that she would give you at time T f(2)=s_up-k dollars if the stock goes up but nothing otherwise and she needs to charge you some amount p now in order to join this game!

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... matures¹⁸

The maturity date of a derivative is the date the buyer of the derivative can (or should) exercise the clauses set by the derivative (usually buying a stock at the strike price k).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... respectively.¹⁹

Therefore, s_up in figure is equal to s₂ here and s_down is equal to s₁.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... question²⁰

The fact is that the financial world treats arbitrage free pricing as an everyday tool for dealing with derivative, but I am just a bit suspicious about this method.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.