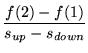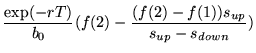

Next: Why is the price
Up: A binomial model for
Previous: A binomial model for
I will introduce a `binomial' model for stock market since it is mathematically simple (but elegant) but still retains the basic things of this topic. (derivative pricing)
Figure:
The `one-step' binomial model for stock market
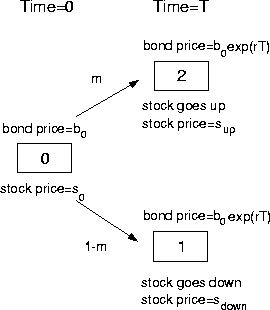 |
In figure ![[*]](cross_ref_motif.gif) , we assume that the transition probability of the stock from s0 to sup is m while from s0 to sdown is (obviously) 1-m. We also assume that the money put in a bank acts predictably with interest rate r. Put the money deposited in a bank in a fancier way: define b0 as the value of a bond at box zero (i.e time zero) so selling a bond means borrowing money while buying a bond means depositing money.
Therefore, the two financial instruments we can handle are stocks and bonds.
Now the only question we are interested is:
, we assume that the transition probability of the stock from s0 to sup is m while from s0 to sdown is (obviously) 1-m. We also assume that the money put in a bank acts predictably with interest rate r. Put the money deposited in a bank in a fancier way: define b0 as the value of a bond at box zero (i.e time zero) so selling a bond means borrowing money while buying a bond means depositing money.
Therefore, the two financial instruments we can handle are stocks and bonds.
Now the only question we are interested is:
Given a derivative that has a payout7 (at time T) of f(2) dollars when the stock goes up and f(1) dollars when the stock goes down, how much8 does it worth?9
First I want to give you the result and then proceed to the argument!
- 1.
- Let
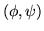 10 be the unit of stocks and bonds one holds respectively. These two values are the so-called contents of a portfolio.
10 be the unit of stocks and bonds one holds respectively. These two values are the so-called contents of a portfolio.
- 2.
- The cost of this portfolio at time zero is
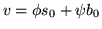 .
.
- 3.
- Let
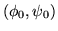 be the solution of the set of the simultaneous equations11
be the solution of the set of the simultaneous equations11
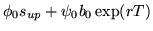 |
= |
f(2) |
(2) |
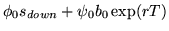 |
= |
f(1) |
(3) |
- 4.
- Upon solving
![[*]](cross_ref_motif.gif) and
and ![[*]](cross_ref_motif.gif) , we would get
, we would get
- 5.
- Then the price, p, of this derivative must be
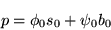 |
(6) |
In other words,
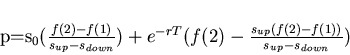 |
(7) |


Next: Why is the price
Up: A binomial model for
Previous: A binomial model for
Birger Bergersen
1998-12-22
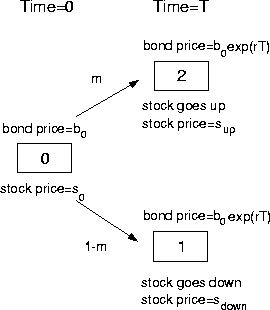
![[*]](cross_ref_motif.gif) , we assume that the transition probability of the stock from s0 to sup is m while from s0 to sdown is (obviously) 1-m. We also assume that the money put in a bank acts predictably with interest rate r. Put the money deposited in a bank in a fancier way: define b0 as the value of a bond at box zero (i.e time zero) so selling a bond means borrowing money while buying a bond means depositing money.
Therefore, the two financial instruments we can handle are stocks and bonds.
Now the only question we are interested is:
, we assume that the transition probability of the stock from s0 to sup is m while from s0 to sdown is (obviously) 1-m. We also assume that the money put in a bank acts predictably with interest rate r. Put the money deposited in a bank in a fancier way: define b0 as the value of a bond at box zero (i.e time zero) so selling a bond means borrowing money while buying a bond means depositing money.
Therefore, the two financial instruments we can handle are stocks and bonds.
Now the only question we are interested is:
![[*]](cross_ref_motif.gif) and
and ![[*]](cross_ref_motif.gif) , we would get
, we would get