

Next: Acknowledgements
Up: The basics of derivative
Previous: A `two-step' model, an
An open question: is arbitrage free pricing foolproof?
If you are careful enough to observe the results we have derived so far by arbitrage free pricing, you will notice that all of them are independent of the transition probability (for example m in figure ![[*]](cross_ref_motif.gif) ). Therefore, by preventing people manipulate stocks and bonds in advance to getting risk free profit via derivatives, we are sacrificing the true probabilistic aspect of the stock itself. It seems to me that it would lead to a paradoxical situation. Let me explain this by an (certainly not so realistic) example.
Referring to the situation of figure
). Therefore, by preventing people manipulate stocks and bonds in advance to getting risk free profit via derivatives, we are sacrificing the true probabilistic aspect of the stock itself. It seems to me that it would lead to a paradoxical situation. Let me explain this by an (certainly not so realistic) example.
Referring to the situation of figure ![[*]](cross_ref_motif.gif) and suppose r=0, let m, the true transition probability from 0 to 1 (i.e. from s0 to sup), be
and suppose r=0, let m, the true transition probability from 0 to 1 (i.e. from s0 to sup), be 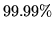 .
Let s0=2 and
sup=1000 and
sdown=1. Suppose someone offers you an option with the strike price k=2. Therefore,
f(2)=1000-2=998 and f(1)=0. By equation
.
Let s0=2 and
sup=1000 and
sdown=1. Suppose someone offers you an option with the strike price k=2. Therefore,
f(2)=1000-2=998 and f(1)=0. By equation ![[*]](cross_ref_motif.gif) , we would get
p=2.998999. This means for a price
p=2.998999 dollars you are almost sure you can buy a stock which worths 1000 dollars for k=2 dollars! Surely you cannot arrange to manipulate your portfolio to gain risk free profit via the option but you nevertheless have a very high chance (
, we would get
p=2.998999. This means for a price
p=2.998999 dollars you are almost sure you can buy a stock which worths 1000 dollars for k=2 dollars! Surely you cannot arrange to manipulate your portfolio to gain risk free profit via the option but you nevertheless have a very high chance (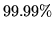 )
of buying an (soon to be) expensive stock at an ultra low cost! I think I am going to leave this as an open question20 for you (and me) to think about...
)
of buying an (soon to be) expensive stock at an ultra low cost! I think I am going to leave this as an open question20 for you (and me) to think about...


Next: Acknowledgements
Up: The basics of derivative
Previous: A `two-step' model, an
Birger Bergersen
1998-12-22
![[*]](cross_ref_motif.gif) ). Therefore, by preventing people manipulate stocks and bonds in advance to getting risk free profit via derivatives, we are sacrificing the true probabilistic aspect of the stock itself. It seems to me that it would lead to a paradoxical situation. Let me explain this by an (certainly not so realistic) example.
Referring to the situation of figure
). Therefore, by preventing people manipulate stocks and bonds in advance to getting risk free profit via derivatives, we are sacrificing the true probabilistic aspect of the stock itself. It seems to me that it would lead to a paradoxical situation. Let me explain this by an (certainly not so realistic) example.
Referring to the situation of figure ![[*]](cross_ref_motif.gif) and suppose r=0, let m, the true transition probability from 0 to 1 (i.e. from s0 to sup), be
and suppose r=0, let m, the true transition probability from 0 to 1 (i.e. from s0 to sup), be ![[*]](cross_ref_motif.gif) , we would get
p=2.998999. This means for a price
p=2.998999 dollars you are almost sure you can buy a stock which worths 1000 dollars for k=2 dollars! Surely you cannot arrange to manipulate your portfolio to gain risk free profit via the option but you nevertheless have a very high chance (
, we would get
p=2.998999. This means for a price
p=2.998999 dollars you are almost sure you can buy a stock which worths 1000 dollars for k=2 dollars! Surely you cannot arrange to manipulate your portfolio to gain risk free profit via the option but you nevertheless have a very high chance (