

Next: A binomial model for
Up: Two similar games in
Previous: JUST a slightly reworded
Think about this: Suppose I am selling you this offer for k dollars. Then I have to give you the stock at time T, what I could have done (among many methods) is that:
- 1.
- borrow s0 dollars at time zero and buy 1 share of stock.
- 2.
- put the stock into my safe until time T.
- 3.
- at time T, I give you the stock, you give me money (k dollars).
- 4.
- but I have to pay back my loan at time T, which is
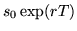 ,
so if I set
,
so if I set
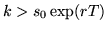 then I am sure I will earn money without any risk. (the keyword here is `without any risk')
then I am sure I will earn money without any risk. (the keyword here is `without any risk')
How about you, the buyer of this offer? Let's take a look on what you could have done if
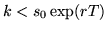 .
.
- 1.
- at time zero you would accept the offer at price k dollars (to be paid at time T).
- 2.
-
also at time zero, sell the stock you are going to have at time T4 at any price
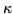 such that
such that
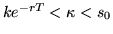 .
(Anyone will buy this since this price is LESS than the stock price!)
.
(Anyone will buy this since this price is LESS than the stock price!)
- 3.
- put the money mentioned in
![[*]](cross_ref_motif.gif) in a bank and at time T you will have
in a bank and at time T you will have
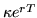 .
.
- 4.
- but you will (at time T) have to pay k dollars to the seller of the offer (i.e. me); nevertheless, you still makes a net profit of
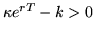 without any risk.
without any risk.
Conclusion: The CORRECT answer for k in game ![[*]](cross_ref_motif.gif) is
is
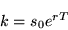 |
(1) |
The above formula is right since we have to make sure that no one makes any profit risk free.5
With this discovery, correct pricing of derivatives6 just reduces to the modelling of stock market and trying to find a portfolio that exactly simulates the payout of the derivative.


Next: A binomial model for
Up: Two similar games in
Previous: JUST a slightly reworded
Birger Bergersen
1998-12-22
![[*]](cross_ref_motif.gif) in a bank and at time T you will have
in a bank and at time T you will have
![[*]](cross_ref_motif.gif) is
is