JUST a slightly reworded version of the previous game!!!

We are at time t=0. You want to do some sort of investment and you have decided to buy stocks. Suppose that the stock price for today is s₀¹, someone offers you to sell you the stock at time T (T>0) for k dollars. (That is, you pay k dollars at time T and get the stock a time T, but the amount k is determined at time zero). How much do you want to pay? (That is, what is k?). Of course we have to assume that the interest rate² is r and the stock price follows a certain probability distribution. `Answer': In the sense of the game mentioned in section , we can deduce the following:

1.

the potential payout of the person who sells you the offer is (S_T-k).

2.

by the time value of money, this potential payout at time zero would have been $\exp(-rT)(S_{T}-k)$.

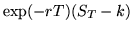3.

we have to set the average (i.e. expectation value) of the random variable 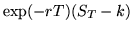$\exp(-rT)(S_{T}-k)$ to zero. In other words, one has 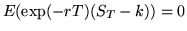$E(\exp(-rT)(S_{T}-k))=0$. (E is the expectation value operator, it takes the average of the random variable inside the bracket).

4.

so we have k=E(S_T). (Take the exponential thing, a constant, out of the expectation operator and note that k is also a constant!)

5.

Conclusion: k is the average value of the stock at time T.

All the derivations seem fine, at least the `answer' has the same appearance of game , but is it the true answer...

NO!!!³