

Next: An open question: is
Up: A binomial model for
Previous: Something mathematical!
How about if we allow time to grow? Let us look at figure ![[*]](cross_ref_motif.gif) :
:
Figure:
The `two-step' binomial model for stock market
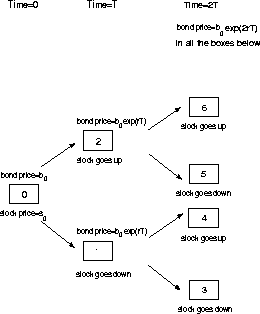 |
Let the stock price at box i be si. If, when the derivative matures18 at time 2T, it has a payout of
f(i), i=3, 4, 5, 6 respectively.19 What is the price of this derivative at time zero?
Answer: It is easy to handle this problem with the redefined probability q. We let
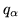 be this `probability' from 0 to 2;
be this `probability' from 0 to 2; 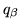 be the `probability' from 2 to 6;
be the `probability' from 2 to 6;
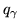 be the `probability' from 1 to 4.
Doing the thing backwards, we have:
be the `probability' from 1 to 4.
Doing the thing backwards, we have:
| f(2) |
= |
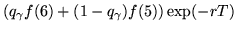 |
(9) |
| f(1) |
= |
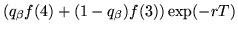 |
(10) |
where f(2) and f(1) are the prices of that derivative at time T if the stock prices are s2 and s1 respectively.
With f(2) and f(3), we can get f(1) which is...
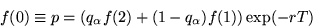 |
(11) |
Note that
f(2), f(3), f(4) are generally different, so in most cases if we create a hedging portfolio at time zero, we have to look at how the stock behaves (whether it is at s1 or s2) and changes the content of the portfolio at time T to make the cost of the content of the portfolio at time T be f(1) or f(2) respectively.


Next: An open question: is
Up: A binomial model for
Previous: Something mathematical!
Birger Bergersen
1998-12-22

![[*]](cross_ref_motif.gif) :
: