PHYS 350 - 2005W [Week 4]

Navigation BarHome PageSyllabusBibliographyProblem SetsNewsContact Info

By week:

You can find the lecture notes at this link or at the Wiki.

Week 4 - Dissipative Systems [3] [5]

Summary

Let's examine how we include friction in our lovely Lagrangian formulation.

Reading List

  • ``Lagrangian Dynamics''
    REF: Wells, D. A. 1967, Chapter 6. Top

Problem Set - 14 October 2005 - Answers

Problem 1 - Schaum 6.1 Top

A small sphere is suspended from a rubber band in a viscous liquid. Assuming a simple viscous force acting on the sphere and no drag on the band, show that generalized viscous force corresponding to the spherical coordinates r, θ, φ are
Fr = - a dr
dt		 , Fθ = -a r2 dθ
dt		 , Fφ = -a r2sin2 θ dφ
dt
Do not use the power function to do this. Use the partial derivatives describing the change from Cartesian to spherical coordinates.

Problem 2 - Schaum 6.17 Top

Find the power function for the Problem 1 and determine the generalized forces conjugate to the spherical coordinates.

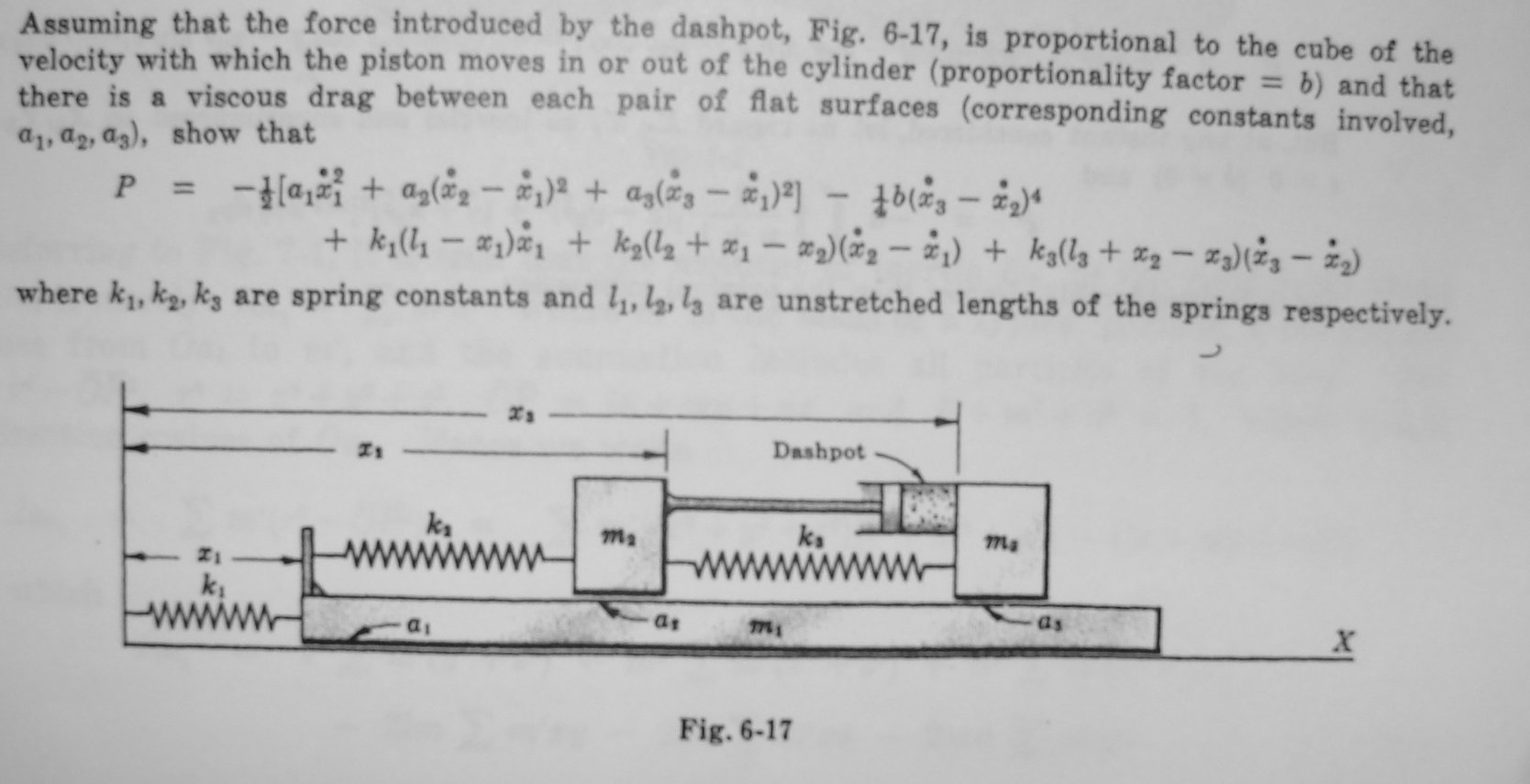
Problem 3 - Schaum 6.26 Top

Last modified: Wednesday, 30 November 2005 12:14:26