You can find the lecture notes at this link or at the Wiki.
Due 21 September 2005 - Answers
Problem 1 - Conical Spiral 
Wells : Problem 3.5.
A bead of mass m is constrained to move along a smooth
conical spiral. The radius of the spiral ρ = a z and the
angle along the spiral φ = - b z where ρ, φ and
z are the standard cylindrical coordinates. Find the
equation of motion of the bead.
Problem 2 - Sprung Pendulum
Wells : Problem 3.7.
A pendulum bob of mass m is suspended by an inextensible
string from the point p. This points is free to move along a
straight horizontal line under the action of the springs each having a
constant k. Assume that the mass is displced only slightly
from the equilibrium position and released. Neglecting the mass of
the springs, find the period of oscillation of the pendulum.
Problem 3 - Bead on a Loop
Wells : Problem 3.12
A bead of mass m is free to move on a smooth circular
wire which is rotating with constant angular velocity ω about a
vertical axis perpendicular to the face of the loop and passing
through its periphery. Another bead is moving under the action of
gravity along an identical loop which is stationary and in a vertical
plane. Prove that both beads have exactly the same motion. What
quantity in the equation of motion for the first bead corresponds to
g in the second equation of motion.
Problem 4 - Barbell
Goldstein : Problem 1.10
Two points of mass m are joined by a rigid weighless rod of
length l, the center of which is constrained to move on a
circle of radius a. Set up the kinetic energy of the system in
generalized coordinates.
Due 28 September 2005 - Answers
Problem 1 - Great Circle
Show that the shortest (or longest) line connecting two points on a
sphere is a segment of a great circle
Problem 2 - Spring
A mass m attached to a coil spring having a constant k, oscillates along a smooth horizontal line with a motion given by
x = A sin ω t where ω = (k/m)1/2. Assuming a varied path represented by
x = A sin ω t + ε sin 2 ω t,
show that for the actual path taken over the interval t=0 to
t=π/2ω (one fourth of a complete oscillation),
/ t=π/2ω
|
/ t=0
|
δL dt = 0
|
and that for the varied path this integral is equal to 3/8 mπωε2.
Problem 3 - Power Lines
Write an integral to calculate the total potential energy of a cable of
mass M and length L that follows a curve y(x). Find the
function y(x) that minimizes the potential energy.
Problem 4 - Fermat's Principle
Fermat's principle states that light takes the path that minimizing
the time to travel between two points. In a medium of index of
refraction n light travels at a velocity c/n in a
straight line. Use Fermat's principle to derive Snell's Law, i.e that
at an interface between materials with indicies of refraction
n1 and n2, the angle that the
light makes with respect to normal on each side of the interface is
n1 sin &theta1
= n2 sin &theta2
Due 7 October 2005 Answers
Problem 1 - Schaum 5.1
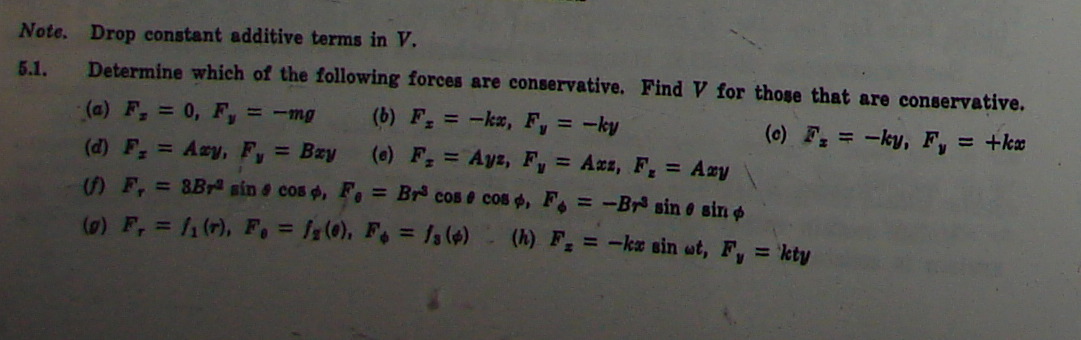
Problem 2 - Schaum 5.5
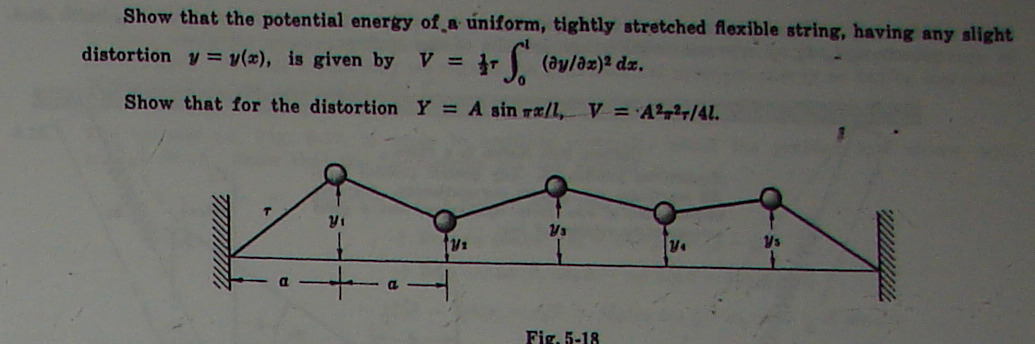
Problem 3 - Schaum 5.12
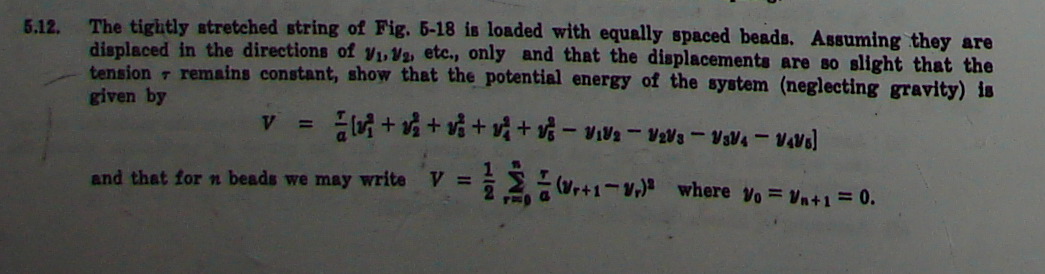
Due 14 October 2005 - Answers
Problem 1 - Schaum 6.1
A small sphere is suspended from a rubber band in a viscous liquid.
Assuming a simple viscous force acting on the sphere and no drag on
the band, show that generalized viscous force corresponding to the
spherical coordinates r, θ, φ are
| Fr = - a |
dr
dt |
, Fθ = -a r2 |
dθ
dt |
, Fφ = -a r2sin2 θ |
dφ
dt |
Do not use the power function to do this. Use the partial derivatives
describing the change from Cartesian to spherical coordinates.
Problem 2 - Schaum 6.17
Find the power function for the Problem 1 and determine the generalized forces
conjugate to the spherical coordinates.
Problem 3 - Schaum 6.26
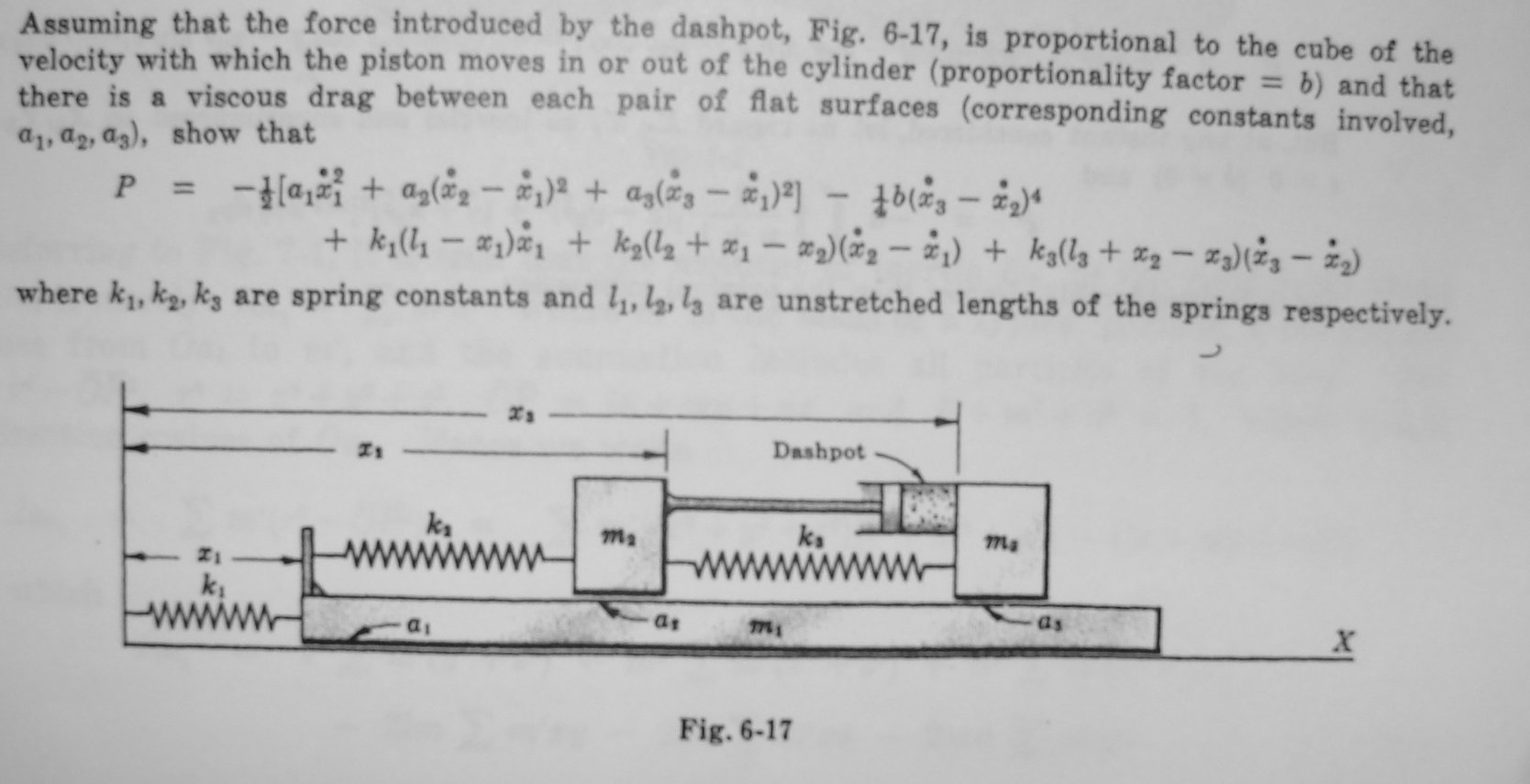
Due 21 October 2005 Answers
Problem 1 - Schaum 7.3
Show that the moment of interia of a body about any line Oa through the origin of coordinates is given by
IOa = (Ix x2
Iy y2
Iz z2
- 2 Ixy xy
- 2 Ixz xz
- 2 Iyz yz
) ( x2 + y2 + z2 )-1
where x,y,z are the coordinates of any point on Oa.
Problem 2 - Cone
Find the moments of inertia of a cone of height h, radius of
the base R, and mass M about the center of mass. What
are the moments of interia about the tip of the cone? What are they about the center of the base?
Problem 3 - Three Rods
Show that a system of three thin rods (of arbitrary length and mass)
is equimomental to any object.
Due Optional Problems Answers
Problem 1 - Marble and Bowl
A marble of mass M and radius r rolls without slipping on the
inside surface of a spherical bowl of radius R. You can assume that
angular velocity of the marble at any moment is parallel to the
surface of the bowl (ω &cdot R=0) where R
is a radial vector between the centre of the spherical bowl and the
point where the marble makes contact with the bowl). The only
external force is gravity.
What is the moment of inertia of the marble about an axis passing
through its centre of mass (assume that the density of the marble is
uniform)? What is the total kinetic energy of the marble as it moves
along the surface of the bowl?
What is the Lagrangian for the marble? What quantities are conserved
during the particle's motion? Write out the equations of motion for
the marble. What is the frequency of small oscillations about the
point of equilibrium? What does the particle's trajectory look like
for these small oscsillations?
Problem 2 - Back to UPS
The UPS depot at YVR has a series of conveyor belts. Sometimes to aid
in sorting, a package is transferred from one belt to another. A
metal bar drops to impede the motion of the package along the first
belt, and a piston pushes the package onto a second belt going
perpendicular to the first belt. Both belts travel at the same
velocity and have the same coefficient of kinetic friction (dry
friction). You may assume that the frictional force between the belt
and the box is proportional to the fraction of the box on the belt.
Write out the equation of motion for the box (assume the box is
rectangular and aligned in the direction of the motion of the belts).
If you neglect the acceleration of the box, you can solve for the
velocity of the box as a function of the fraction of the box on each
belt. Integrate up the velocity to find the time as a function of position.
Problem 3 - Battle Bot
A four-wheeled remote control vehicle is fitted with a large counterrotating drum.
The angular velocity of the drum is horizontal and perpendicular to
the direction of the vehicle's motion. The top of the drum moves so
that is velocity is opposite to the forward velocity of the vehicle.
Explain why steering the vehicle is unstable when the vehicle is going
forward and statble when the vehicle is going backward.
Due 4 November 2005 Answers
Problem 1 - Like a rubber ball ...
When a rubber ball bounces, it rolls without slipping at the point of
contact between the ball and the floor. This means that the point of
contact is stationary at the moment of contact. Assume that energy is
conserved by the bounce.
Derive a relationship between the initial velocity and angular
velocity of the ball and the final velocities. What combination of
initial velocities result in an exact reversal of the velocities of
the ball (angular and linear)? If you sets things up like this the
ball will bounce back and forth between two fixed points.
Problem 2 - Flippin' coin
When you flip a coin such that the rotational axis almost
perpendicular to the face of the coin, how fast does the Queen's head
spin compared to rate at which the coin wobbles?
Problem 3 - Torquing Planet Earth
Derive an equation for the total potential energy of a body whose
centre of mass lies a distance R from a point mass m.
Expand this expression to second order in l/R where l is
the size of body. You should find a term proportional to
R-1 and a term proportional to
R-3. There is no R-2 term. The
first term should be familar, and you can write the second one in
terms of the moments of inertia of the body. Use this to estimate
the rate of precession of the Earth's rotation axis due the torques
exerted by the moon and sun. We are looking for an order of magnitude
estimate, so assume that the torque is about equal to the second-order
potential energy (the R-3 term) and that the angular
momentum of the Earth is simply Iz2π/(1 day).
The precession rate is the total torque (sun plus moon) divided by the
angular momentum; you will find that the answer only depends on the
ratios of the various moments of inertia of the Earth, the mass of the
sun and moon, and the distances to the sun and moon.
You may find the following Taylor series helpful.
(1+x)-1/2 = 1 - x/2 + 3/8 x2 + O(x3)
Also to translate your answer to some number of years, you will find the
following facts helpful.
G (M1 + M2)
R3
|
= (The angular velocity of an orbit)2.
|
We derived this in class. The mass of the Sun is 333,000 times that
of the Earth. The mass of the Earth is 81 times that of the Moon.
I got to within a factor of three of the actual precession rate, so this rough calculation is pretty good.
Due 18 November 2005 Answers
Problem 1 - Funny Car
One of the classic types of funny car is one in which the rear
suspension has a lot of bounce. Although I'm not certain how this is
achieved, let's analyze the normal modes of oscillation of a car's
suspension and try to figure out how to give it the biggest bounce at
the rear end.
Let's model the suspension and the car as a metal rod of length
L. At each end of the rod is a spring. The spring constants
are k1 and k2. The centre of mass of the car is located a distance l from spring #1 and the mass of the car is given by M. You can ignore the mass of the rod and the springs.
Determine the potential energy of the car in terms of the extension of
the springs. For argument's sake let's take the metal bar to be
horizontal when there is no load on it and use x1
and x2 to denote the vertical position of each end
of the bar relative to the unloaded position. What are the equilibrium values of x1 and x2 as a function of l, L, M and the spring constants?
Expand the potential and kinetic energy about x1
and x2 and determine the normal modes of oscillation
of the car. How can we increase the oscillation of the rear end by
moving the centre of mass? How can we do it by adjusting the suspension (the spring constants)?
Problem 2 - Springy Bob
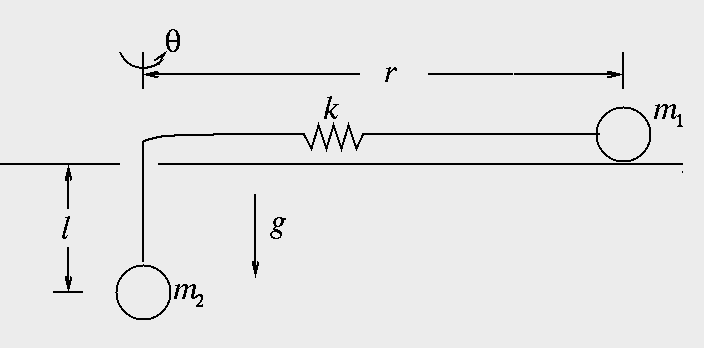Two masses are connected by a spring and a string. Take the total
length of the unstretched spring and string to be given by b.
Mass #1 is restricted to move in a horizontal plane and mass #2 can
only move vertically.
What is the Lagragian for the system? Find a steady solution to
equations of motion. This means that l and r are constant
with time but θ may have a constant velocity.
What is the equation of motion for small perturbations on the steady motion?
How is the perturbed motion similar to epicycles?
Due 25 November 2005 Answers
Problem 1 - Steel Drum
A steel drum consists of the sawed off bottom of a steel barrel. The
bottom of the barrel is hammered into a portion of a sphere.
Bumps of various sizes are hammered into the spherical surface.
Check out
this link
for more information.
What changes would you make to the analysis of membranes that we
presented in class?
Problem 2 - A Real Drum
In class we analyzed the modes of oscillation of a drum with a square
membrane. In reality most drums are round. Write the equation of
motion of the membrane in cylindrical coordinates and substitute a
trial solution of
z(r,θ t) = R(r) f(θ) g(t)
You should get a differential equation for the three functions.
For the square-top drum head the three functions were all sines and cosines.
Here you will get something different.
To solve the differential equations, divide both sides of the equation
of motion by the trial solution z(r,θ t). You should find that
the second derivative of f divided by f is a constant (not a function
of f) - similarly for g. What types of functions satisfy these
formulae? Now you know f(θ) and g(t).
For the final function we have
1
R(r)
|
/
|
\
|
d2 R(r)
d r2
|
+ |
1
r
|
d R(r)
d r
|
\
|
/
|
= -A2 +
|
n2
r2
|
This differential equation has the solution
R(r) = Jn ( A r )
where J is a Bessel Function of the First Kind.
What is the significance of the constant A? If I hit the drum
in the exact center, what is the ratio of the frequency of the second
and first harmonic to the fundamental? Is it 5:3:1 like when I pluck a string in the middle or hit a square drum in the middle?
What if I hit the drum in a random spot?
Use the website above (and here) to figure this out.
Draw nodal diagrams for the fundamental and first two overtones in both cases.
Due 2 December 2005 at 1pmHere are the rules. If you do better on this assignment than the midterm the scaled mark for this assignment will replace that of the midterm. If in the opinion of the instructor you have collaborated, your assignment will be shredded before it is graded. This determination will be final and without appeal (we have a crosscut shredder). You have nothing to lose by doing the assignment and nothing to gain if you collaborate.The assignment will cover material from the entire course up to 30 November 2005. The questions will be revealed at 1pm on 30 November 2005. Although the instructor may find queries on the assignment submitted after 1:10pm on 30 November 2005 entertaining, he will not entertain them.
Problem 1 - Question The First
Calculate the moment of inertia of a solid, regular hexagonal prism about its symmetry axis. Express your answer in terms of the
mass of the prism and the length of each side.
Problem 2 - Question The Second
A uniform solid cylindrical drum of mass M and radius a is free to rotate about its axis, which is horizontal. A cable of negligible mass and equilibrium length l0 is wound on the drum, and carries on its free end a mass m. Write down the Lagrangian function in terms of appropriate generalized coordinates. You may assume that the cable does not slip on the drum and that the cable is elastic with a potential energy 1/2 k x2. Find and solve the equations of motion assuming that the mass is released from rest with the cable unextended.
Problem 3 - Question The Third
Find the normal modes of oscillation of two pendulums of different masses M and m but the same length l. Both pendulums are attached to the same horizontal bar; the points of attachment are separated by a distance s0. The pendulums are connected by a spring with spring constant k. When both masses are at the bottom of their arcs, the spring has its equilibrium length.
Problem 4 - Question The Fourth
Write down the kinetic energy of a particle in cylindrical polar
coordinates in a frame rotating with angular velocity ω about
the ''z''-axis. Show the the terms proportional to
ω and ω2 reproduce the Coriolis
force and the centrifugal force respectively.
Last modified: Wednesday, 30 November 2005 12:14:25
| 
