You can find the lecture notes at this link
or at the Wiki.
Week 9 - Perturbed Motion
Problem Set
Problem 1 - Funny Car 
One of the classic types of funny car is one in which the rear
suspension has a lot of bounce. Although I'm not certain how this is
achieved, let's analyze the normal modes of oscillation of a car's
suspension and try to figure out how to give it the biggest bounce at
the rear end.
Let's model the suspension and the car as a metal rod of length
L. At each end of the rod is a spring. The spring constants
are k1 and k2. The centre of mass of the car is located a distance l from spring #1 and the mass of the car is given by M. You can ignore the mass of the rod and the springs.
Determine the potential energy of the car in terms of the extension of
the springs. For argument's sake let's take the metal bar to be
horizontal when there is no load on it and use x1
and x2 to denote the vertical position of each end
of the bar relative to the unloaded position. What are the equilibrium values of x1 and x2 as a function of l, L, M and the spring constants?
Expand the potential and kinetic energy about x1
and x2 and determine the normal modes of oscillation
of the car. How can we increase the oscillation of the rear end by
moving the centre of mass? How can we do it by adjusting the suspension (the spring constants)?
Problem 2 - Springy Bob
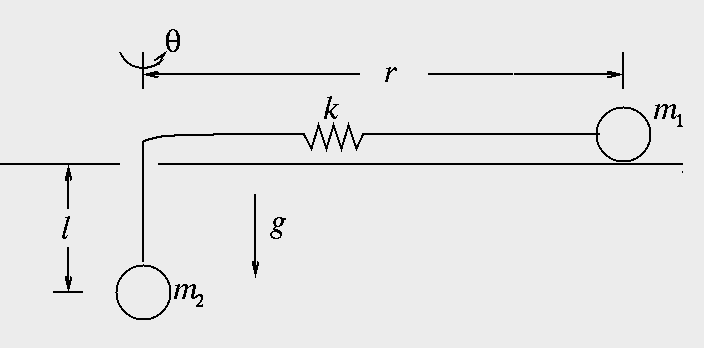Two masses are connected by a spring and a string. Take the total
length of the unstretched spring and string to be given by b.
Mass #1 is restricted to move in a horizontal plane and mass #2 can
only move vertically.
What is the Lagragian for the system? Find a steady solution to
equations of motion. This means that l and r are constant
with time but θ may have a constant velocity.
What is the equation of motion for small perturbations on the steady motion?
How is the perturbed motion similar to epicycles?
Last modified: Wednesday, 30 November 2005 12:14:24
| 
