ASTR 304 - 2009W [Answers for Week 2]

Navigation BarHome PageSyllabusBibliographyProblem SetsNewsContact Info

By week:

Week 2 - Rotation-Powered Neutron Stars

Problem Set

Problem 1 - Spinning Neutron Stars Top

We will estimate how quickly we would expect neutron stars to spin, how much energy is stored in their spin and other interesting facts about spinning neutron stars.

  1. The sun rotates every 24-30 days depending on latitude. How quickly would it rotate if it were compressed to 10km in radius while conserving its angular momentum? Its current radius is 7 x 1010 cm.
  2. How fast could a neutron star rotate without breaking up? Consider the neutron star to be 1.4 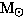and have a radius of 10 km and compare the centripetal acceleration of a bit of material on the surface to the gravitational acceleration.
  3. How much angular momentum and rotational energy does a neutron star have? Use
    I ≈ 0.21
    M R2
    1-2 G M
    R c2
    4. and a spin period of break-up, 1.6 ms, 33 ms and 6 s.

Answer for Problem 1

  1. The angular momentum of a rotating body is proportional to M R2 P-1, so if R deceases by a factor of 7 x 104, its period will decrease by the square of that factor, so P ≈ 0.44 ms.
  2. Breaking up is hard to do.
    G M
    R2     		= 4 π2 R
    P2     		so P2= 4 π2 R3
    G M
    Substituting the numbers yields about 0.46 ms.
  3. First we will calculate I. The formula above yields 1 x 1045 g cm2. The angular momentum is simply I Ω and the energy is ½ I &Omega2

    L = 6 x 1045 P-1 erg s and E = 2 x 1046 P-2 erg where P is the period in seconds.

    PLE
    0.44ms1.4 x 10491 x 1053
    1.6ms4 x 10488 x 1051
    33ms2 x 10472 x 1049
    6s1 x 10456 x 1044

Problem 2 - Original Spin Top

If you know the age of a neutron star, its current period and its period derivative, you can estimate its original spin.

  1. Using the results from the lectures, derive a formula for P0 in terms of the age, current period and period derivative of a pulsar.
  2. The table below lists pulsars that are associated with historical supernovae. Complete the table by calculating the original spin of these neutron stars.
    Name Age [yr] Period [s] P-dot [10-15 s s-1] P0 [s]
    B0531-21 949 0.0331 422.69  
    B0540-69 1000 0.050 480  
    B1951+32 64000 0.0395 5.8  
    J0205+6449 822 0.06568 193  
  3. Why do we know the age of the first and last pulsars so accurately?

Answer for Problem 2

  1. P0=(P2-2 τ P P-dot)1/2 = P (1-2 τ/T)1/2
    where &tau is the age of the pulsar and T is the characteristic age, T=P/P-dot. If τ << T, then the pulsar's period hasn't changed much since it was born (which makes a whole lot of sense).
  2. Filling out the table with the formula:
    Name Age [yr] Period [s] P-dot [10-15 s s-1] P0 [s]
    B0531-21 949 0.0331 422.69 0.016
    B0540-69 1000 0.050 480 0.031
    B1951+32 64000 0.0395 5.8 0.025
    J0205+6449 822 0.06568 193 0.060
    Notice that none of them started their dipole spin-down at zero period. This could mean that the neutron stars were born spinning slowly or perhaps something else slowed them down at the beginning like gravitational radiation.
  3. They are associated with historical supernovae that were first seen on July 4, 1054 (now the Crab Nebula or M1) and August 6, 1181 (now the SNR 3C 58).
Last modified: Thursday, 08 April 2010 14:15:28