


Next: About this document ...
Up: Boltzmann statistics
Previous: Partition function and the
For an isolated system
S=S(E,V,N), with E,V,N independent
variables. For a system in contact with a heat bath at a
given temperature, T becomes an independent variable, or control
parameter. The energy E and entropy S will then fluctuate about
their mean values
 and
and
 .
E and
S become dependent variables
given by equations of state. The change of variables is handled most
efficiently by introducing
he Helmholtz free energy. In thermodynamics it is defined
as
.
E and
S become dependent variables
given by equations of state. The change of variables is handled most
efficiently by introducing
he Helmholtz free energy. In thermodynamics it is defined
as
F=E-TS
Imagine a reversible process which takes the system
from one equilibrium state to another
We see that the Helmholtz free energy is should be considered to be dependent on the control variables T,V,N.
We have
In statistical mechanics we define the Helmholtz free energy as
We wish to show that for a large system
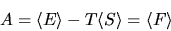 |
(19) |
Proof:
The canonical partition function is
![\begin{displaymath}
=\int {{dE}\over{\delta E}}\exp\left\{\beta[E-TS(E,V,N)]\right\}\end{displaymath}](img60.gif) |
(20) |
We evaluate this integral using the
saddle point method.
Almost all the contribution to the integral will come from values
of E near
 the value for which
E-T(S,E,V,N) = minimum. We let
the value for which
E-T(S,E,V,N) = minimum. We let
 and
and
Substituting (![[*]](cross_ref_motif.gif) ) into (
) into (![[*]](cross_ref_motif.gif) ) we obtain
) we obtain
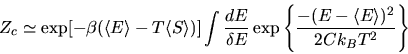 |
(21) |
Using (![[*]](cross_ref_motif.gif) )
we find
)
we find
and from (![[*]](cross_ref_motif.gif) )
)
![\begin{displaymath}
A=-k_BT\ln Z_c=\langle E\rangle -T\langle S\rangle -k_BT\ln
\left[{{\sqrt{2
\pi k_BT^2C}}\over{\delta E}}\right]\end{displaymath}](img66.gif) |
(22) |
The last term in (![[*]](cross_ref_motif.gif) ) will be small compared to the first two
terms for a large system, and it is possible to choose the tolerance
) will be small compared to the first two
terms for a large system, and it is possible to choose the tolerance
 so that it is identically zero. We have therefore shown
that (
so that it is identically zero. We have therefore shown
that (![[*]](cross_ref_motif.gif) ) is correct.
) is correct.



Next: About this document ...
Up: Boltzmann statistics
Previous: Partition function and the
Birger Bergersen
1998-09-14
![[*]](cross_ref_motif.gif) ) into (
) into (![[*]](cross_ref_motif.gif) ) we obtain
) we obtain
![[*]](cross_ref_motif.gif) )
we find
)
we find
![[*]](cross_ref_motif.gif) )
)
![[*]](cross_ref_motif.gif) ) will be small compared to the first two
terms for a large system, and it is possible to choose the tolerance
) will be small compared to the first two
terms for a large system, and it is possible to choose the tolerance
![[*]](cross_ref_motif.gif) ) is correct.
) is correct.