Boltzmann factor

Consider now a system in contact with a heat bath, or reservoir. System 1 is the one we are interested in, and we want to find the probability P(E₁) that it has energy E₁. We assume that system 2 is much larger than 1, so that E₁<< E=E₁+E₂. Another way of putting this is to say that the heat capacity C₂ of system 2 is very large. We assume that all compatible microstates are equally likely. We have

$$P(E_1)dE_1={{g_1(E_1)g_2(E-E_1) dE_1}\over{ \int dE_1g_1(E_1)g_2(E-E_1)}}$$

From the definition of entropy

$$g_2=\frac{1}{\delta E}\exp\left[{{S_2(E-E_1)}\over{k_B}}\right]$$

We expand in a Taylor series

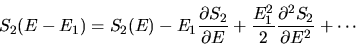$$S_2(E-E_1)=S_2(E)-E_1{{\partial S_2}\over{\partial E}}+{{E_1^2}\over{2}}{{\partial^2S_2}\over{\partial E^2}}+\cdots$$ (13)

With T the temperature of the heat bath and C its heat capacity, the partial derivatives are given by

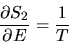$${{\partial S_2}\over{\partial E}}={{1}\over{T}}$$ (14)

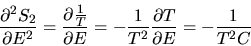$${{\partial^2S_2}\over{\partial E^2}}={{\partial {{1}\over{T... ...1}\over{T^2}}{{\partial T}\over{\partial E}}=-{{1}\over{T^2C}}$$ (15)

Since E₁<<TC we neglect the last term in () giving

$$g_2=const. \exp\left[{{-E_1}\over{k_BT}}\right] =const. e^{-\beta {E_1}}$$

where we define $\beta =1/(k_BT)$ . We conclude

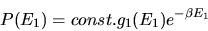$$P(E_1)= const. g_1(E_1)e^{-\beta {E_1}}$$ (16)

The factor $e^{-\beta {E_1}}$ is the Boltzmann factor. When a system is in contact with a heat bath at a certain temperature, all possible microstates of the system are no longer equally likely. Instead, the Boltzmann factor acts as a weight factor biasing the distribution towards states with lower energy.