• Summary
• Reading List
• Problem Set
• Answers

Week 5 - Accreting Neutron Stars [4] [6]

Summary

Many neutron stars are paired with other stars and accrete from their companions. How a neutron star accretes is an interplay between the magnetic field of the neutron star, the evolution of the orbit and the properties of the companion star.

The discovery of planets orbiting other stars is one of the most exciting discoveries of the past decade and a half.

• Monday 1 February Accreting Neutron Stars
• Thursday 4 February Introduction to Exoplanets

Reading List

• ``Disk accretion by magnetic neutron stars''
  [ ADS, PDF ]
  REF: .Ghosh, P., Lamb, F. K. 1978, Astrophys. J. Lett., 223, L83-L87 .

• ``Theory and Observations of Type I X-Ray Bursts from Neutron Stars''
  [ PDF ]
  REF: Bildsten, L. 2000, .

• ``On spherically symmetrical accretion''
  [ ADS, PDF ]
  REF: Bondi, H. 1952, Mon. Not. Royal Astr. Soc., 112, 195-+
  You don't need to read this paper, but I will try to cover it in class.

Problem Set

Problem 1 - Accretion

1. Let's use Newtonian gravity for simplicity here. How much kinetic energy does a gram of material have if it falls freely from infinity to the surface of a star of mass M and radius R?
2. How much energy is released if a gram of material falls from a circular orbit just above the stellar surface onto the stellar surface? To put it another way, what is the kinetic energy of the material in the circular orbit?
3. Hydrogen burning releases about 6 x 10¹⁸ erg/g. How does accretion of hydrogen onto a neutron star (R=10km, M=1.4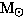) differ from accretion onto a white dwarf (R=10000 km, M=0.6)?
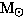4. What is the total about of energy released per gram of material as it falls from infinity to the surface of a neutron star? How many grams of material would have to fall each second on the neutron star to generate an Eddington luminosity through accretion? This is called the Eddington accretion rate.

Problem 2 - Bursts

We will try to model Type-I X-ray bursts using a simple model for the instability. We will calculate how much material will accumulate on a neutron star before it bursts.

1. Let us assume that the star accretes pure helium, that the temperature of the degenerate layer is constant down to the core (T_c), how much luminosity emerges from the surface of the star? (You shouldn't have to derive this formula (I gave it to you in class).
2. Let us assume that the helium layer has a mass, dM, and that the enregy generation rate for helium burning is given by

   ε3α = 3.5 x 1020 T9-3 exp(-4.32/T9) erg s-1 g-1

   where T₉=T/10⁹K. The energy generation rate is a function of density too, but let's forget about that to keep things simple. How much power does the helium layer generate as a function of dM?
3. Equate your answer to (1) to the answer to (2) and solve for dM. This is the thickness of a layer in thermal equilibrium.
4. Let's assume that the potential burst starts by the temperature in the accreted layer jiggling up by a wee bit. If the surface luminosity increases faster with temperature than the helium burning rate, then the layer is stable. Calculate dL_surface/dT and dP_helium/dT.
5. Calculate the value of dM for which dP_helium/dT exceeds dL_surface/dT and the layer bursts.
6. Equate your value of dM in (3) and (5) and solve for T. What is dM? How long will it take for such a layer to accumulate if the star is accreting at one-tenth of the Eddington accretion rate?