By week:
|

Week 3 - The Structure of Neutron Stars
Problem Set
Problem 1 - Newtonian Polytropes 
We are going to do some dimensional analysis to understand stars with a
polytropic equation of state, polytropes.
-
Consider a star of mass, M, and radius, R. Construct by dimensional analysis
a characteristic pressure and a characteristic density from these quantities
and Newton's constant, G.
-
A polytropic equation of state is a power-law relationship between pressure
and density, P = K ρα. Substitute the characteristic
pressure and density into the polytropic equation of state to derive a
mass-radius relation.
-
Which values of α have special properties? What are they?
Answer for Problem 1
-
The key to doing the dimensional analysis is check out what you have first.
The density part is easy M/R3. The pressure part is somewhat
more difficult. GM/R is an energy per unit mass, so GM2/R is
an energy and finally GM2/R4 is a pressure.
-
Let's substitute the characteristic density and pressure into the
polytropic equation of state.
G M2
R4
|
~ K |
Mα
R3α
|
so |
G M2-α
K
|
~
R4-3α
|
The ~ sign means that the two sides are equal up to a dimensionless
number. This number may be a function of other dimensionless quantities
in the problem. For this problem, the number is a function of α. It
vanishes for α=6/5, so this polytrope has a infinite radius for any
finite mass.
-
If α=4/3, M is not a function of R. This is where the Chandrasekhar
limit comes from as a relativistic degenerate gas has α=4/3. If
α=2, R is not a function of M. This solution is important for neutron
stars because over an important range of densities, the nuclear equation
of state has α=2 so for neutron stars over an interesting range of mass
R is a function of K, i.e. it is a direct probe of the equation of state.
Problem 2 - Central Pressures 
We will calculate the central pressure of a incompressible star in
Newtonian physics and general relativity.
-
Use the General Relativistic equations of hydrostatic equilibrium
to determine the
central pressure of a star of mass M and radius R. The material is
incompressible, i.e. its density is constant. After integrating (9) from the
center where the enclosed mass, u, vanishes, it is easiest to integrate (10)
from the surface where the pressure vanishes. Write your answer as a function
of M and R by eliminating the constant density from the result.
-
By dimensional analysis, figure out where the factors of G and c appear in
the General Relativistic equations of hydrostatic equilibrium.
-
Derive the Newtonian equations of hydrostatic equilibrium by taking the limit
of c → ∞.
-
Redo the pressure calculation in Newtonian physics.
-
By dimensional analysis, figure out where the factors of G and c appear in
your answer to (1).
-
Check your answers by taking the limit of c → ∞ for your answer
to (5) and comparing it with the answer to (4).
-
What is the minimal radius for a constant-density star
of a given mass? What is the maximal mass for a star of a particular density?
What is the maximal mass for a star at nuclear density, 1015 g cm-3?
Answer for Problem 2
-
The hydrostatic equilibrium equations are given by equations (9) and (10)
in Oppenheimer and Volkoff.
Equation (9) is easy to integrate, yielding u = 4/3 π r3 ρ
or more conveniently,
Equation (10) is a bear though. Even though it is quite ugly, the
differential equation is separable and integrable. Here goes
d P
d r
|
= − |
P + ρ
r ( r - 2 u )
|
( 4 π P r3 + u )
|
I am going to substitute the results for u.
Rearranging to integrate and using the definition of ρ yields
d p
4 π (P+ρ)(P+ρ/3)
|
= − |
r d r
|
Both sides integrate to logarithms. After exponentiating both sides and
doing some cancelations we get
The constant of integration A is set by exploiting the fact the P=0
at r=R, so
Because we are interested in the central pressure, we can set r=0 giving,
P + ρ
P + ρ/3
| = 3 ( 1 - | 2 M
R |
)1/2 |
Using the fact the gravitational redshift at the surface is given by
1 + z = (1 - 2M/R)-1/2, gives a simple expression for the
central pressure
Putting in the dependence on M and R gives a much less attractive expression
|
P(r=0) = |
3M
4π R3 |
[R ( R-2M )]1/2 + 3 M - R
4 R - 9 M |
-
There are no factors of c or G required in equation (9). Equation (10)
looks like
d P
d r
|
= − |
P + ρ c2
r ( r - 2 G u/c2 )
|
( 4 π P r3 + u c2 )
|
G
c2 |
-
In the Newtonian limit, the two equations are
| u = 4 π r2 ρ and |
d P
d r
|
= − |
G u ρ
r2
|
-
The equations here are really straight forward and yield
-
I am going to use the expression with the gravitational redshift, so
ρ becomes ρ c2
-
As c → ∞, z vanishes as c-2, so if I use
the first order expansion for z, i.e. z = G M / R c2, I
get the central pressure to be,
|
P(r=0) = |
G M ρ
2 R |
= |
3
8 π |
G M2
R4 |
-
The minimum radius is R = 9/4 M. The maximum mass for a particular
density is
or about 3.6
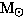 for ρ = 1015 g cm-3. for ρ = 1015 g cm-3.
Problem 3 - Neutron Star Masses 
Calculate from dimensional analysis the typical mass of a neutron star.
-
Use the characteristic density and pressure of a star that you derived in Problem 1.
Neutron stars have relativistic neutrons so the pressure is about the density times
c2. Use this to derive a relationship between the mass and radius of the
star.
-
A relativistic degenerate gas has a density of one particle in a cube a Compton wavelength
on a side. Combine this with the result from Part 1 to solve for the mass of the star.
Answer for Problem 3
- The characteristic pressure and densities are GM2/R4
and M/R3 yielding,
G M2
R4
|
~ |
M
R3
|
c2 so |
G M
R c2
|
~
1
|
-
Continuing,
|
ρ ~
|
m4 c3
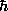 3 3
|
~ |
M
R3
|
so M ~ |
(c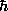 )3/2 )3/2
G3/2 m2
|
= M3Planck m-2 |
If you use the mass of the neutron you get 3.7 x 1033g or
1.9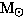 . .
Last modified: Thursday, 08 April 2010 14:15:28
|