
Week 1 - The Discovery of Neutron Stars
Problem Set
Problem 1 - The Eddington Luminosity 
There is a natural limit to the luminosity a gravitationally bound
object can emit. At this limit the inward gravitational force on a
piece of material is balanced by the outgoing radiation pressure.
Although this limiting luminosity, the Eddington luminosity, can be evaded
in various ways, it can provide a useful (if not truly firm) estimate
of the minimum mass of a particular source of radiation.
-
Consider ionized hydrogen gas. Each electron-proton pair has a mass
more or less equal to the mass of the proton (mp)
and a cross section to radiation equal to the Thompson cross-section
(σT).
-
The radiation pressure is given by outgoing radiation flux over the speed
of light.
-
Equate the outgoing force due to radiation on the pair with the inward force
of gravity on the pair.
- Solve for the luminosity as a function of mass.
The mass of the sun is 2 x 1033 g. What is the Eddington
luminosity of the sun?
Answer for Problem 1
The outgoing flux is given by
This yields a outgoing force of
| frad = |
F σT
c |
= |
L σT
4 π r2 c |
Meanwhile the force due to gravity is
Setting the sum of forces to zero and solving for L yields
| LEdd = |
4 π c G M mp
σT |
= 1.3 x 1038 erg s-1 |
M
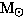 |
Problem 2 - Minimum Masses 
The observations of Sco X-1 can give a
lower limit on the mass of the sources if they are gravitationally bound.
The source discovered by Giacconi et al. is now known as Sco X-1.
- What is the most likely distance to Sco X-1 given its location on the
sky?
-
At this distance given the flux estimate in the Giacconi et al., what
is the luminosity of Sco X-1?
-
What is the minimum mass of Sco X-1?
The distance to Sco X-1 is still not well determined.
Answer for Problem 2
Sco X-1
-
Because the source is so close in the sky to the galactic center, a good
guess for its distance is the distance to the center of the galaxy, 10 kpc.
-
The paper quotes a flux of about 5 photons cm-2s-1 at
a wavelength of 3 Å. This gives an energy flux of 3.3 x 10-8
erg cm-2s-1. Using 10 kpc as the distance yields a
luminosity of 4 x 1039 erg/s.
-
Using the Eddington luminosity calculated in Problem 1 yields a mass estimate
of 3
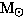 . .
Last modified: Thursday, 08 April 2010 14:15:28
|