

Next: Subrecoil cooling and Lévy-flights
Up: Two sub-recoil cooling methods
Previous: Velocity selective coherent population
-Works for three-level atoms
Uses stimulated Raman transitions.
Level scheme:
Two laser beams with different frequencies
 from opposite directions
from opposite directions
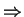 absorption from one beam, stimulated emission into the other
absorption from one beam, stimulated emission into the other
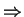 total momentum transfer=
total momentum transfer=
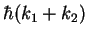
Very small linewidth of Raman transitions
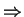 only talk to narrow velocity class of atoms around v0
only talk to narrow velocity class of atoms around v0
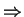 control v0 by detuning
control v0 by detuning
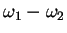
Cooling scheme:
- 1.
- Sequence of pulses with different negative detunings
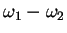 from left, giving atoms with v<0 kick to the right.
from left, giving atoms with v<0 kick to the right.
- 2.
- optically pump atoms back with pulse of light at real transition. Spontaneous emission randomizes velocity distribution
- 3.
- repeat sequence 1) with positive detunings from the right, giving atoms with v>0 kick to the left
- 4.
- optically pump atoms back
By using different pulse sequences (detuning, power, and pulse shapes) one can tailor a velocity-dependent excitation probability for atoms around v=0.
Same situation achieved as in VSCPT:
Excitation probability P(v) with dip at v=0 and randomizing diffusion process that allows atoms to fall into the (v=0)-trap.
Note: Trap is not a real trap (only v-dependence, no dependence on x)


Next: Subrecoil cooling and Lévy-flights
Up: Two sub-recoil cooling methods
Previous: Velocity selective coherent population
Birger Bergersen
1998-12-12
![\includegraphics[height=12cm,width=12cm,angle=90]{ramscheme.ps}](img31.gif)
![\includegraphics[height=12cm,width=12cm,angle=90]{ramscheme.ps}](img31.gif)
![\includegraphics[height=12cm,width=12cm,angle=-90]{rampuls.ps}](img35.gif)