

Next: About this document ...
Up: No Title
Previous: Raman cooling
In both subrecoil schemes had excitation probability P(v) with dip at v=0
p=0: Dark state
p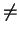 0: Momentum diffusion which transfers atoms into dark state
0: Momentum diffusion which transfers atoms into dark state
Fluorescence rate dependence on momentum:
(=excitation probability)
The smaller p the longer the delay between successive spontaneous emissions
Estimate efficiency of cooling process:
Define trapping zone
p<ptrap.
Atoms remain trapped for time 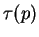 of order
1/RF(p).
of order
1/RF(p).
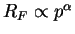 for small p (
for small p (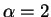 for VSCPT)
for VSCPT)
Evolution of an atom:
successive trapping periods
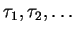
diffusion periods
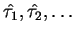 (first return times)
(first return times)
Consider 2N alternating trapping and diffusion periods
Total trapping time = T(N) =
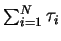
Total escape time =
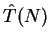 =
=
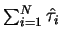
How do T(N),
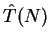 grow with N?
grow with N?
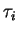 ,
,
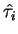 independent random variables
independent random variables
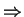 need to find probability distributions P(
need to find probability distributions P(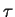 ),
),
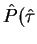 )
)
Introduce distribution 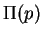 : Distribution of p for atoms that fall into the trap.
: Distribution of p for atoms that fall into the trap.
Atoms trapped if
p<ptrap,
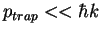 , but p-distribution of recoil has width of order
, but p-distribution of recoil has width of order 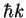
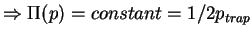
Calculate P(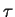 ) asymptotically for large
) asymptotically for large 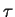 :
:
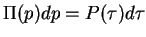
(Trapping probability,
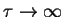 for
for
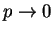 )
)
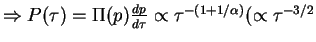 for
for
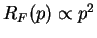 )
)
Broad distribution of trapping times,
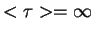
T(N) is Lévy-sum: T(N)
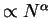 (
(
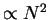 for
for
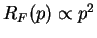 ) for large N.
) for large N.
Sum dominated by largest term, i.e. longest trapping time is of the order of total observation (or interaction) time
How about escape times?
Different models to consider:
- 1.
- atomic momentum confined to
|p|<pmax (e.g. friction mechanism at large p)
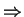 have mean value for first return times to the trap
have mean value for first return times to the trap
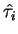 of the order of diffusion time from 0 to pmax
of the order of diffusion time from 0 to pmax
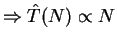
- 2.
- constant fluorescence rate for large p (in real situation: pe large )
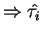 coincide with first return times of Brownian motion
coincide with first return times of Brownian motion
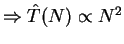
- 3.
- realistic RF(p) as in figure (probed for long interaction times)
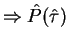 even broader,
even broader,
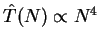
Conclusion for cooling efficiency in the three models:
- 1.
- T(N) dominates over
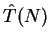 for large N, all atoms get trapped
for large N, all atoms get trapped
- 2.
- T(N) and
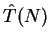 both
both
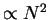 (for
(for
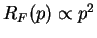 ), finite fraction of atoms get trapped.
), finite fraction of atoms get trapped.
- 3.
-
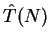 dominates over T(N), atoms lost from trap for long interaction times
dominates over T(N), atoms lost from trap for long interaction times
Cooling in 2 and 3 dimensions:
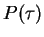 becomes narrower
becomes narrower
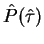 becomes broader
becomes broader
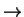 cooling efficiency decreases
cooling efficiency decreases
For
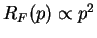 get
get
d=2:
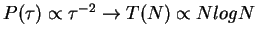
d=3:
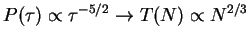
Raman cooling:
Can tailor excitation probability, i.e. manipulate 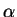 in
in
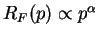 (by choice of pulse shapes)
(by choice of pulse shapes)
Which 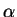 leads to most effective cooling (both accumulation of atoms in trap and lowest achievable temperature)?
leads to most effective cooling (both accumulation of atoms in trap and lowest achievable temperature)?
Got effective friction mechanism for large p
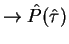 is narrow distribution
is narrow distribution
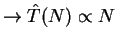
 need
need
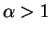 to accumulate atoms into trap
to accumulate atoms into trap
On the other hand:
Found that longest trapping time 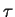 is of the order of total interaction time
is of the order of total interaction time 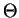 and the corresponding momentum of the atom is a measure for width of the resulting momentum distribution
and the corresponding momentum of the atom is a measure for width of the resulting momentum distribution
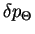 , i.e. the temperature of the atoms:
, i.e. the temperature of the atoms:
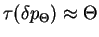
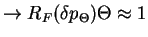
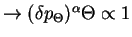
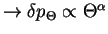
For given interaction time:
The smaller 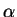 is chosen the colder the atoms get.
Together with efficiency considerations: Want
is chosen the colder the atoms get.
Together with efficiency considerations: Want 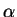 close to but greater than 1.
close to but greater than 1.
First experiments used so-called Blackman pulses that have
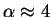 (chosen to minimize side bands).
(chosen to minimize side bands).
Square pulses (in time domain) lead to
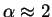 .
.
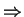 New temperature record of 3 nK (compared to 100 nK before) was achieved with help of Lévy-flight analysis of the problem.
New temperature record of 3 nK (compared to 100 nK before) was achieved with help of Lévy-flight analysis of the problem.
Conclusions:
- Introduced basic theory of Doppler cooling
- Explained two methods of sub-recoil cooling
- Showed how the cooling process can be described in terms of Lévy-flight statistics
- Drew conclusions about efficiency of the cooling process
References:
Doppler cooling: '' Optical molasses'', P.D. Lett et al., J. Opt. Soc. Am. B, 6 (1989) 2084
VSCPT: ''Laser cooling below the one-photon recoil energy by velocity-selective coherent population trapping'', A. Aspect et al., Phys. Rev. Lett. 61 (1988) 826
Raman cooling: ''Laser cooling below a photon recoil with three-level atoms'', M. Kasevich and S. Chu, Phys. Rev. Lett. 69 (1992) 1741
Lévy flights: ''Subrecoil laser cooling and Lévy flights'', F. Bardou et al., Phys. Rev. Lett. 72 (1994) 203
''Raman cooling of Cesium below 3 nK: New approach inspired by Lévy flights statistics'', J. Reichel et al., Phys. Rev. Lett. 75 (1995) 4575
Click here for Return to title page


Next: About this document ...
Up: No Title
Previous: Raman cooling
Birger Bergersen
1998-12-12
![\includegraphics[height=12cm,width=12cm,angle=-90]{model1.ps}](img37.gif)
![\includegraphics[height=12cm,width=12cm,angle=-90]{model1.ps}](img37.gif)
![\includegraphics[height=12cm,width=9cm,angle=90]{levy3.ps}](img38.gif)
![\includegraphics[height=12cm,width=10cm,angle=-90]{model2.ps}](img67.gif)