ASTR 304 - 2003W [Week 10]

Navigation BarHome PageSyllabusBibliographyProblem SetsNewsContact Info

By week:

Week 10 - Supermassive Black Holes [9] [11]

Summary

Supermassive black holes fuel the brightest persistent sources in the universe, quasars. We will explore the rich phenomenology of quasars and their cousins, the connection between black holes and the galaxies in which they reside and what quasars can well us about galaxy formation.

Reading List

  • ``A Structure for Quasars''
    [ ADS, PDF ]
    REF: Elvis, M. 2000, Astrophys. J., 545, 63-76 . Top

Problem Set

Problem 1 - Accretion-Disk Efficiency Top

Let's assume that an accretion disk extends from infinity down to some rA.
  1. Using Newtonian gravity, how much energy is released per unit mass as material spirals to the inner edge of the disk?
  2. Now using general relativity, redo the calculation. Assume that the central object is a non-rotating black hole. The energy released per unit mass is given by 1-ut where uα is the four-velocity of material in the disk and you are using the Schwarzschild metric.
  3. In general relativity, an accretion disk can only extend down to R=6M around a non-rotating black hole. What is the efficiency of accretion onto such a black hole?

Problem 2 - Holes v. Stars Top

I have claimed in class that accretion produces a large fraction of the light in the universe. You are going to see if this holds water.

It turns out that the masses of black holes in the centers of galaxies is well correlated with the mass of the bulge of the galaxy (if it is a spiral galaxy) or the entire galaxy if it is an elliptical: MBH ≈ 0.016 Mbulge.

  1. Let's take a bulge of 108 . If the black hole was built up by accretion over the age of the universe, what would its average luminosity be? Let's assume that it is a Schwarzschild hole.
  2. The mass-to-light ratio of the bulges of galaxies is given by
    Mb
    Lb     		= 0.0776 /
    |
    \    		 Lb
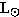
    		\0.18
    |
    /
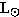
    What is the luminosity of the stars in bulge?

Problem 3 - Our Very Own Supermassive Black Hole Top

Andrea Ghez's group at UCLA constructed this beautiful movie of the centralmost arcsecond of our Galaxy. The edge of the box measures on arcsecond on the sky.

  1. Use the movie to estimate the mass of the black hole at the center of our Galaxy.
  2. How many Schwarzschild radii does the closest star approach the black hole?
  3. How big would the black hole look on the sky to the hapless inhabitants on a planet orbiting this star? Would it be as big as the moon, Jupiter, Mars?
  4. You have probably assumed something about the orbit of one of the stars. What did you assume? How does the mass of the black hole change if you vary this assumption? What could Andrea's team do to tighten the estimate of the black hole mass?
Last modified: Tuesday, 06 April 2004 07:28:12