By week:
|

Week 1 - The Discovery of Neutron Stars, Black Holes and Gamma-Ray Bursts
Problem Set
Problem 1 - The Eddington Luminosity 
There is a natural limit to the luminosity a gravitationally bound
object can emit. At this limit the inward gravitational force on a
piece of material is balanced by the outgoing radiation pressure.
Although this limiting luminosity, the Eddington luminosity, can be evaded
in various ways, it can provide a useful (if not truly firm) estimate
of the minimum mass of a particular source of radiation.
-
Consider ionized hydrogen gas. Each electron-proton pair has a mass
more or less equal to the mass of the proton (mp)
and a cross section to radiation equal to the Thompson cross-section
(σT).
-
The radiation pressure is given by outgoing radiation flux over the speed
of light.
-
Equate the outgoing force due to radiation on the pair with the inward force
of gravity on the pair.
- Solve for the luminosity as a function of mass.
The mass of the sun is 2 x 1033 g. What is the Eddington
luminosity of the sun?
Answer for Problem 1
The outgoing flux is given by
This yields a outgoing force of
| frad = |
F σT
c |
= |
L σT
4 π r2 c |
Meanwhile the force due to gravity is
Setting the sum of forces to zero and solving for L yields
| LEdd = |
4 π c G M mp
σT |
= 1.3 x 1038 erg s-1 |
M
 |
Problem 2 - Minimum Masses 
The observations of Sco X-1 and the quasars 3C 48 and 3C 273 can give a
lower limit on the mass of the sources if they are gravitationally bound.
The source discovered by Giacconi et al. is now known as Sco X-1.
- What is the most likely distance to Sco X-1 given its location on the
sky?
-
At this distance given the flux estimate in the Giacconi et al., what
is the luminosity of Sco X-1?
-
What is the minimum mass of Sco X-1?
The distance to Sco X-1 is still not well determined.
You can estimate distances to 3C 48 and 3C 273 using the redshift
of the objects. At the time, the Hubble constant was thought to be
around 100 km/s/Mpc. The conventional wisdom is that it is 72 km/s/Mpc.
Feel free to use either value.
-
What are the distances to 3C 48 and 3C 273? Feel free to neglect
cosmological effects (for bonus points use ΩM = 0.3
and ΩΛ=0.7).
-
Do your distances agree with those in the papers?
-
The paper gives estimates of the luminosity in the optical and radio
of these sources. What are the minimum masses of the objects using the
optical and radio luminosities?
Answer for Problem 2
Sco X-1
-
Because the source is so close in the sky to the galactic center, a good
guess for its distance is the distance to the center of the galaxy, 10 kpc.
-
The paper quotes a flux of about 5 photons cm-2s-1 at
a wavelength of 3 Å. This gives an energy flux of 3.3 x 10-8
erg cm-2s-1. Using 10 kpc as the distance yields a
luminosity of 4 x 1039 erg/s.
-
Using the Eddington luminosity calculated in Problem 1 yields a mass estimate
of 3
 . .
Quasars
-
The redshift of 3C 273 is 0.158, a velocity of 47400 km/s, and a distance of
474 Mpc (658 Mpc with H0=72 km/s/Mpc).
The redshift of 3C 48 is 0.3675, a velocity of 110300 km/s, and a distance of 1103 Mpc (1530 Mpc with H0=72 km/s/Mpc).
If you include the cosmological effects you will find a luminosity distance
for 3C 273 which is a factor of 1.116 larger than above. For 3C 48 the
correction is a factor of 1.249. The luminosities will be larger by
the square of these factors.
-
They agree.
-
The luminosity of 3C 273 from the Schmidt paper is 1059ergs
over 105 years which is 3 x 1047erg/s and
an Eddington mass of 2 x 108
 . .
3C 48 emits 4 x 1044 erg/s in the radio which gives
3 x 106 for
the radio Eddington mass. In the optical the paper gives an absolute visual
magnitude estimate -25.2. The sun's absolute visual magnitude is 4.8, so
3C 48 is approximately 1012 for
the radio Eddington mass. In the optical the paper gives an absolute visual
magnitude estimate -25.2. The sun's absolute visual magnitude is 4.8, so
3C 48 is approximately 1012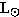 or 107 or 107
Problem 3 - Gamma-ray Burst Energetics 
About how much energy is released in a gamma-ray burst if they are
-
In low Earth orbit?
-
At the distance of the moon?
-
At the disance of Pluto?
-
Near the center of the galaxy?
-
At cosmological distances?
What are the Eddington limiting masses for each of these scenarios? In which
scenarios, would you be surprised if a gamma-ray burst repeated?
Estimate the amount of energy released by the following events. Use
the formula GMm/R.
- A nuclear explosion - 5 kg of fissile plutonium. Each plutonium atom
releases about 200 MeV as it splits.
- The collision of two asteroids. Assume each is 10 km in radius with a
density of 3 g cm-3.
- The collision of two neutron stars.
Assume each is 10 km in radius with a density of
1015 g cm-3.
- The collision of an asteroid with a neutron star.
Which events could explain gamma-ray bursts at the various possible
distances? N.B. Only a fraction of the total energy released will end
up as gamma rays.
Answer for Problem 3
The satellites measured time integrated fluxes ranging from 10-5erg cm-2 to 2 x 10-4erg cm-2.
Energy estimates
The key to these energy estimates is of course the distance to the source.
I will used 5 x 10-5 erg cm-2 for the canonical
integrate flux (or fluence).
-
Because the satellites were also in orbit, it is reasonable to use the
Earth's radius as a distance estimate so d = 6000 km and an energy
of 2.5 x 1014erg. I was rather lax about this distance estimate.
A careful reading of the paper would give a much larger distance of 1.2 x 105 km because the Vela satellites were in rather high orbit themselves
looking down toward the Earth.
-
The Earth-moon distance is 385,000 km, so E = 9 x 1017erg.
-
The distance from Pluto to the Sun is about 6 billion kilometers,
so E = 2 x 1026erg.
-
Let us take the center of the Galaxy to be 10 kpc or 3 x 1022cm,
yielding E=6 x 1041erg.
-
Let us take "cosmological distances" to be something like 10 billion
light-years, E=5 x 1052erg.
Eddington Masses
If you assume that the burst last one to ten seconds, you can obtain
estimates for the mass. For the results below I have used ten seconds.
- 3.84 x 108 g
- 1.38 x 1012 g
- 3.07 x 1020 g
- 4.61 x 103

- 4.61 x 1014

Possible Scenarios
-
Plutonium bomb - Each plutonium atom has an atomic weight of 239, so
1 MeV per nucleon is released or 1.6 x 10-6 erg per nucleon.
5 kg consists of 3 x 1027 nucleons,
yielding 4.8 x 1021 ergs or about 100 kilotons of TNT.
By the way, 5 kg is less than the critical mass of 239Pu, so this
is what you would get from the first 5 kg beyond critical.
-
Collision of two asteroids - 1025 erg, if they hit each other
due to their mutual gravitational interaction, the impact velocity
is only 10 m/s. Two asteroids could be on a collision course with
a much higher relative velocity.
-
Collision of an asteroid with a neutron star - 4 x 1040 erg
-
Collision of two neutron stars - 1054 erg
Last modified: Tuesday, 06 April 2004 07:28:03
|