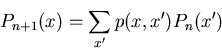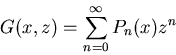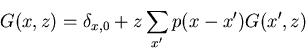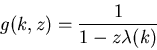

Next: About this document ...
13. Pareto tail. Continuous time random walk.
LAST TIME
- Geordie Rose argued that quantum theory
describes the evolution of the probability amplitude.
- In our treatment based on the master equation
we only discussed the evolution of the probability.
- Neglect of phase coherence justified if
decoherence time short compared with other time scales of interest.
- In this limit we obtained a description where
the different participating
processes took place at Poisson rates.
- Today we will allude to, but not show in detail, that there
are many other processes correlations between successive steps
are important.
- We will continue our discussion of the scaling properties
of the Levy-stable distributions.
- We also start relaxing the assumption of Poisson rates.
NON-GAUSSIAN BEHAVIOR
- In the last but one lecture we showed how
non-Gaussian behavior could be obtained from jump
distributions that had infinite variance
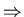 Lévy
flights
Lévy
flights
- In physics Lévy flights with uncorrelated increments are hard to
find because they involve discontinuous processes. We will, however,
later in this course discuss superdiffive processes where
typical displacements increase with time faster than
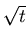 .
.
- Possibly best physical example of levy flights is diffusion in worm-like surfactant
micelles Ott et al. [1990], Cates and Candeau [1990].
- Discontinuous random walks more common in finance, economics and evolution and will be discussed further in Lecture 15.
- Earliest and possibly most best known example of Lévy
stable distributions in finance
 Pareto tail.
Pareto tail.
PARETO TAIL FOR INCOMES
- The income distribution in most
societies is roughly
lognormal for most
people who do have an income, up to approximately the 97th percentile.
- We will later discuss how lognormal
distributions arise in random multiplicative processes.
- The lognormal distributions does not to hold for the 2-3% who are
extremely rich.
Vilfredo Pareto
tried, during the last part of the 19th and the early part of the
20th century, to make economics and sociology into an "exact" science
by pursuing analogies with physics and mechanics. He was particularly
interested into the dynamics of business cycles and the rise and
fall of empires and elites, and his work remains somewhat controversial.
He wrote in
1897 that
In all places and at all times the distribution
of income in a stable economy, when the origin of measurement is
at a sufficiently high income level, will be given approximately
by the empirical formula
y=ax-v, where y is the number of people
having an income x or greater and v is approximately 1.5.
Income tax data in several countries agree qualitatively
with Pareto's observation also in more recent times.
MECHANISM PROPOSED BY LYDALL[1959]
Arrange employees within an
enterprise in a hierarchy.
Let yi be the number of people at the i'th level and let
i+1 be the level above.
The ratio of personnel
at the two levels are
n=yi/yi+1
Suppose each operator on
the i'th level earn their income xi from a commission of a fraction
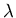 of the income of the people in the level below. In return
a fraction
of the income of the people in the level below. In return
a fraction 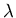 of the income is paid to the immediate boss
above.
of the income is paid to the immediate boss
above.
The income at the i+1 level is thus
If p[x] is the probability distribution for
income
x we have
We find a power law distribution of the Pareto form with
In order for amplification to take place we must impose the restriction
v is the exponent of the cumulative
distribution i.e.
Note that the exponent v is non-universal, and
depends on the parameters n and 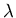 which must be expected
to vary from society to society.
which must be expected
to vary from society to society.
Montroll and Shlesinger [1982][1983] builds a model to explain the data from the observation that
The leverage people in the investment
business have their style of amplification. During certain periods
of prosperity easy money become available for investment, sometimes
in stock, sometimes in real estate or perhaps in silver or Rembrandts.
A common feature of such times is that the daring may exploit the
easy money to acquire some speculative commodity through margin
payment, say, 10% with a promise to pay the remainder. If the commodity
doubles in price a 10% margin is amplified into a ninefold profit.
Let
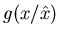 be the basic distribution without amplification.
be the basic distribution without amplification.
With a small probability 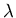 the income is amplified by
leverage N times. The income distribution becomes
the income is amplified by
leverage N times. The income distribution becomes
Asymptotically
Substituting
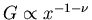 we
find
we
find
The two approaches are mathematically equivalent.
A less tongue in cheek discussion of the income distribution can be found in
Mandelbrot [1962]. This article reprinted commented upon in
Mandelbrot [1997].
Pareto's
own thoughts on the subject can be found in Pareto[1968] and [1984].
RELAXING ASSUMPTION OF INDEPENDENT POISSON RATES:
- Consider cases where waiting time
distribution
in "traps" non-Poisson.
- In financial markets one observes periods with high
volatility and enormous trading volumes interspersed with
slow periods.
- Look at situations where randomness is "quenched" or "frozen".
If system comes back to where it has been before, it finds
the same "randomness" as it found the last time
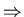 long range correlations.
long range correlations.
- In physical systems examples abound in heterogeneous systems with either
- Wide distribution of trap energies
 amorphous
solds.
amorphous
solds.
- Frozen disorder
 glasses.
glasses.
- Irregular flow fields
 hydrodynamics in heterogeneous media.
hydrodynamics in heterogeneous media.
CONTINUOUS TIME RANDOM WALKS
Consider a walk on a regular lattice
in d-dimensions
Three probability distributions of interest:
- Pn(x)= probability that walker has arrived
at x after n steps, starting at the origin i.e
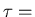 waiting time at each site.
waiting time at each site.
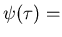 waiting time distribution
waiting time distribution
- P( x,t)= probability that a walker is at
x at time t.
Assume that probability distribution p for jumps in
different directions is given:
For a translationally invariant lattice
equation can be solved using methods of generating functions
and Fourier transforms.
Substituting into recursion relation
g(k) Fourier transform of G(x,z) over lattice.
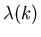 Fourier transform of p( x).
Get
Fourier transform of p( x).
Get
In the limit of an infinite lattice
we then find the lattice Green's function
Where BZ stands for Brillouin Zone. (Readers unfamiliar with
solid state physics can find an excellent introduction in
Ascroft and Mermin [1976]. We will not need to get into
details about reciprocal lattices and lattice sums in this course).
SUMMARY
- Discussed Pareto tail of income distribution.
- Started to discuss situations where individual
processes in master equation were not Poisson distributed.
- Formulated continuous time random walk problem.
- Separated probability distribution after n steps
from distribution after time t.
- The former distribution could be found by
lattice Greens function methods.
Return to title page
14. Return time distribution. Continuous time random walk(continued)


Next: About this document ...
Birger Bergersen
1998-10-28
![\begin{displaymath}v+1={{\ln n}\over{\ln[n\lambda (1-\lambda )]}}\end{displaymath}](img7.gif)