

Next: About this document ...
14. Return time distribution. Continuous time random walk(continued).
LAST TIME
- Started to discuss situations where individual processes
were not Poisson distributed and/or were not independent.
- Introduced "continuous time random walk".
- Interested in the following distributions:
-
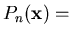 probability that walker has arrived
at x after n steps, starting at the origin.
probability that walker has arrived
at x after n steps, starting at the origin.
-
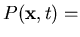 probability that a walker is at
x at time t.
probability that a walker is at
x at time t.
-
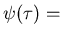 waiting time distribution
waiting time distribution
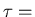 waiting time at each site.
waiting time at each site.
For discussions that follows need the following closely related distributions:
- First passage time distribution
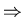 Distribution of n
when system first reaches x starting at the origin.
Distribution of n
when system first reaches x starting at the origin.
- Return distribution
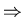 Distribution of n
when system first returns to its starting point.
Distribution of n
when system first returns to its starting point.
- Escape probability
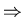 Probability that a system will
never return to starting point.
Probability that a system will
never return to starting point.
Consider walk on
lattice of dimension d, n is the number of jumps:
e vector to near neighbor.
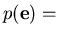 probability of jump to neighbor
probability of jump to neighbor 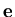 .
.
Write:
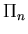 is the first passage time distribution.
is the first passage time distribution.
Assume translational invariance
Introduce generating functions
We find:
Probability that a particle will return to homesite at any time
is
If
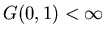 there is a finite escape
there is a finite escape
probability.
If
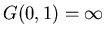 the system will "always" return to the home site
the system will "always" return to the home site
Last time we calculated
where BZ stands for Brillouin zone and
If the walk is unbiased we must have for small values of k
(Technical note: We have implicitly assumed that the walk takes place on a
Bravais lattice for which all lattice sites are equivalent.
There must then be a neighbor -e for every neighbor e
and we can rewrite the defining equation for
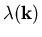
Clearly
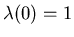 and there will be no odd powered terms in an expansion
of
and there will be no odd powered terms in an expansion
of
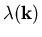 in powers of k. If the lattice is not
Bravais i.e. has a basis we must take into account that there
inequivalent sites in the unit cell of the lattice. The
notational complications this introduces represents an unnecessary
difficulty for our present discussion, in the continuum limit
where the discretenes of the lattice is neglected
in powers of k. If the lattice is not
Bravais i.e. has a basis we must take into account that there
inequivalent sites in the unit cell of the lattice. The
notational complications this introduces represents an unnecessary
difficulty for our present discussion, in the continuum limit
where the discretenes of the lattice is neglected
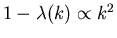 must still hold)
must still hold)
For a d-dimensional lattice
and we conclude that the integral over k
in the expression for
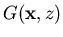 will be divergent for
small k (infrared divergence) for
will be divergent for
small k (infrared divergence) for 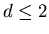 .
.
We conclude:
- For d>2 a particle starting at origin will always escape.
- For
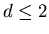 diffusing particles will keep returning
to origin.
diffusing particles will keep returning
to origin.
G(0,1) has been evalauted analytically for the body centered, face centered and simple cubic lattices
The return probability is found to be:
To find the asymptotic behavior of the first return
distribution for 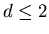 look at how
look at how
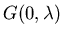 diverges as
diverges as
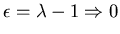
One can show that this means that the
probability that a walk has not yet returned home
after n steps is
Unbiased, continuous, Gaussian, random walk in one dimension
In this case we can calculate the first passage time distribution
explicitly:
Let x1<x<x2. A random walk in one dimension from x1
to x2 must pass through x at least once.
P(x2-x1,t) probability of motion from x1 to x2 in time t
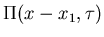 probability of arriving for the first time at x
at time
probability of arriving for the first time at x
at time 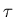 .
.
L(x,u)= Laplace transform of P(x,t)
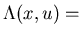 Laplace transform of
Laplace transform of
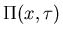
Find
For an unbiased, Gaussian random walk
with Laplace transform
We find
Performing an inverse Laplace transform we find
The first passage time distribution is on the Levy-
Smirnov form for a stable Lévy distribution with
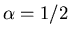 .
We have encountered this distribution before (Lecture 11)
.
We have encountered this distribution before (Lecture 11)
Note that in the continuos case we cannot take the limit
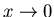 !
!
Returning to the continuous time random walk:distributions Pn(x), P( x,t),
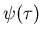
Let us assume that Pn is well behaved
If the waiting time distribution has a mean
successive jumps occur on the average at the rate 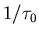 and
and
If the waiting time distribution doesn't have a mean:
the time for n jumps typically
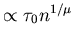
and
Subdiffusive behavior!
Two examples of subdiffusive behavior were discussed in class:
- Photoconductivity in amorphous materials. The example was
taken from Montroll and West [1987], see also Montroll and Scher
and Montroll [1975].
- Diffusion on comb-like structures. The example was taken from
Bouchaud and Georges [1990]
SUMMARY
We have discussed
- The escape probability for diffusion
on a lattice. Found that in one or two dimensions a diffusing particle
will "always" return to home site, but in three or more dimensions
there is a nonzero probability of escape.
- The return distribution in one and two dimensions.
- The first passage time distribution for continuous random
walk in 1-d.
- Anomalous diffusion when waiting distribution
did not have a mean.
Return to title page
15. Random walk in fractal time. Correlated walks


Next: About this document ...
Birger Bergersen
1998-10-28
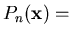 probability that walker has arrived
at x after n steps, starting at the origin.
probability that walker has arrived
at x after n steps, starting at the origin.
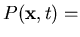 probability that a walker is at
x at time t.
probability that a walker is at
x at time t.
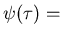 waiting time distribution
waiting time distribution
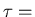 waiting time at each site.
waiting time at each site.
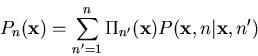
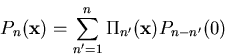
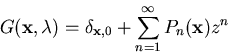
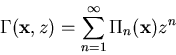
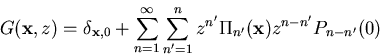
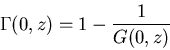
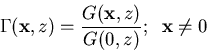
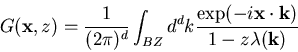
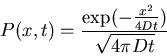
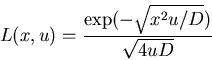
![\begin{displaymath}\Pi(x,t)=\frac{1}{t}\sqrt{\frac{x^2}{4\pi Dt}}\exp[-\frac{x^2}{4Dt}]\end{displaymath}](img51.gif)