EXAMPLE ROTATION QUESTIONS:
1)
A car accelerates with constant acceleration from rest to 10 m/s and
then remains at a constant speed. Sketch graphs of the angular
position, angular velocity and angular acceleration of one of its
wheels.
2) Do the same for the angular position, angular velocity and
angular acceleration of a ball that rolls part way up a ramp and
then back down
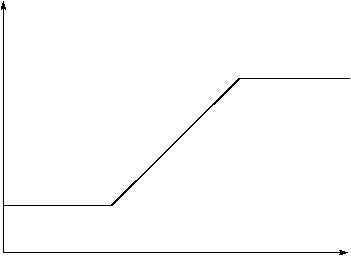
4)
Give a description (in words) of the rotational motion of an
object whose angular position vs time graph is the one shown below:
5)
Give a description (in words) of the rotational motion of an
object whose angular velocity vs time graph is the one shown above.
6)
If the graph above represents the angular velocity vs time and the
object starts at angular position 0, draw the angular acceleration vs
time graph and the angular position vs
time graph.
7) A wheel's angular position as a function of time is theta = (2 s-3) t3. What is the angular position, angular velocity, and angular acceleration of the wheel at t = 2s?
8)
The angular position of a ball is given by the graph in question 4, where the
initial and final angular positions are pi/4 and 3 pi/4 and the change happens
between 4s and 6s. What are the angular position, angular velocity and angular acceleration at
5s?
9)
In the angular velocity vs time graph below, which is greater, the
instantaneous acceleration at 5s or the average acceleration between 0 and 5 s.

12)
Suppose the graph above represents angular position vs time. If the function is a parabola
and the angular position at 5s is pi/3 (the angular position is 0 at time 0). What is the instantaneous angular velocity at
time 5s, and what is the average angular velocity between 0 and 5s?
13) The data below represent the angular position of an object at times
0,0.01s,0.02s,0.03s,0.04s,0.05s,0.06s,0.07s,0.08s,0.09s,0.1s. Estimate
the instantaneous angular velocity and acceleration at time 0.05s.
3,3.02,3.08,3.18,3.32,3.50,3.72,3.98,4.28,4.62,5
14)
A 1 kg solid sphere or radius 10cm rotates at angular speed 10s-1. Calculate the magnitude of angular momentum.
15)
A planet of mass M moves in a a circular orbit of radius R and
period T around a star. Calculate the angular momentum of the planet
around the star.
16)
Describe an experiment that can be used to determine the relative moment of inertia
of two objects (without weighing and measuring them).
17) Does conservation of angular momentum imply that rotational velocity of an isolated system can never change? Explain.
18) A
solid disk of radius 1m and mass 1kg rotates once per second on a
frictionless axle. A small sticky object of mass 10g travels at 10m/s
directly towards the center of the disk (in the plane of the disk). The
sticky object collides and sticks to the edge of the disk. What is the
angular velocity of the ball plus disk after the collision? 19)
A solid disk of radius 1m and mass 1kg rotates once per second on a
frictionless axle. Another non-rotating disk with radius 1m and mass
2kg is dropped on top of the first one. The two disks slip against each
other for a while, but then start rotating together. What is the final
angular speed of the pair of disks?
20) A solid disk of
radius 1m and mass 1kg sits stationary on a
frictionless axle. A bullet of mass 1g and speed 100 m/s is fired
toward the edge of the disk and moves (in the same plane as the disk)
on a trajectory that would take it 0.5m from the center of the disk. If
the bullet hits and sticks in the disk, what is the angular speed of
the disk after the collision.
21) Give an example of a rotating object whose angular momentum is not conserved.
22)
A 10m long pole of mass 10kg is attached to the ground on its bottom
end but its other end is free to move around. If the pole is tilted to
a 30 degree angle from the vertical, what will be the instantaneous
angular acceleration of the pole as it falls toward the ground (Hint:
what is the torque on the pole about the axis of rotation) (Hint for
the hint: what is the axis of rotation in this problem)?
23)
A cylindrical drill bit of mass 20g, length 5cm and radius 0.3cm
rotates at a constant speed of 2000rpm. What is the net torque on the
drill bit?
24) Tiger Woods misses an easy putt and
throws his golf club into the air. Does F=ma still apply in this
situation since the golf club is spinning around and not well
represented by a particle?
25) Someone hands you a hollow sphere
and a solid sphere, each with the same mass and radius. How could you
tell which one is solid?
26) When the pole in question 22 hits the ground, what is its angular velocity (hint: think energy conservation)?
27)
An astronaut in the space shuttle swings a ball around on a 1 meter
long rope. If the ball goes around once per second and the mass of the
ball is 100g, what is the tension in the rope?
28) Determine the
orbital speed of a planet of mass m around a star of mass M if it
orbits in a circular orbit at a distance R from the center.

