

Next: About this document ...
Problem set 2:
Consider a chemical reaction in which a
certain species X is produced at a steady
rate
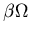 .
If two molecules collide they
produce a new inert substance which is removed from
the system
.
If two molecules collide they
produce a new inert substance which is removed from
the system
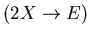 .
Let the collision rate be
.
Let the collision rate be
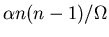 .
The reactions are irreversible and
we write the master equation on the form
.
The reactions are irreversible and
we write the master equation on the form
Where E is the raising (or creation) operator.
- Carry out a system size expansion of the master equation to derive a Fokker-Planck equation for
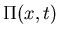 where
where
- Find the steady concentration
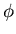 and the
variance of x to leading order in
and the
variance of x to leading order in 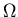 .
.
- The problem is actually exactly solvable
using the method of characteristics discussed in Lecture 6.
The solution is outlined in a paper by Mazo [1975].
Fill in the steps of Mazo's calculation and show
that the Fokker-Planck equation and the exact solution
agree to leading order. In particular justify the boundary
conditions for the generating function!
- Find the correction of order unity to the mean number
of X molecules.
Return to table of content
Birger Bergersen
1998-10-08