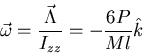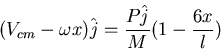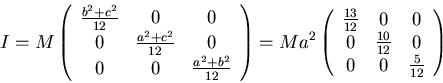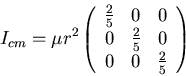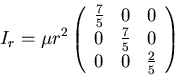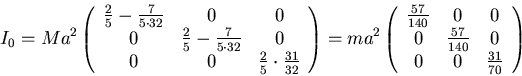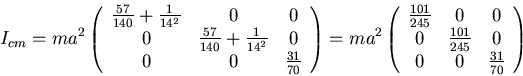

Next: About this document ...
PHYSICS 206
Problem set 6 1999, solution
Problem 1
Introduce a coordinate system as in figure:
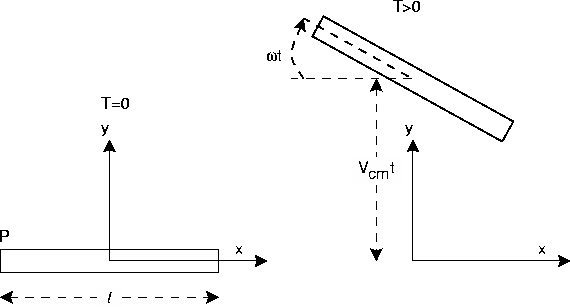
The z-axis points out of the plane of the paper.
The moment of inertia about a vertical axis through the
center of mass is
a:
The center of mass velocity is
while the angular momentum is
so that the angular velocity is
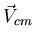 and
and
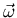 stay constant during the subsequent motion, since no further forces or torques act on the plank.
stay constant during the subsequent motion, since no further forces or torques act on the plank.
b:
The translational velocity of the point of contact is
The position of the point of contact P at time t is
The velocity of 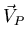 is thus
is thus
The angular velocity
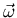 is independent of the reference point.
is independent of the reference point.
c:
The position of an arbitrary point on the plank which initially was
located a distance x to the right of the center of mass is
The initial velocity of this point is thus
We conclude that the initial velocity is zero a distance
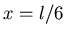 to the right of the center on mass.
to the right of the center on mass.
Problem 2
The moments of inertia of a box with sides a,2a,3a about
the center of mass in a coordinate system with axes parallel to the
sides of the box is
We have
The kinetic energy is thus
Problem 3
The moment of inertia of a sphere of radius r, mass 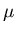 about its center is
about its center is
The moment of inertia tensor of the same sphere about (0,0,-r) is
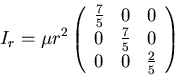 |
(1) |
Let M be the mass of the solid sphere in the absence of a cavity
and m the mass with the cavity present. We have
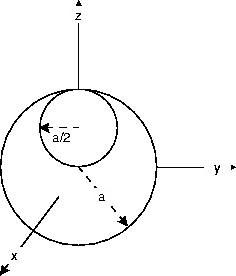
a:
The
z-coordinate of the center of mass is
b:
Substituting
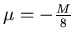 and
and
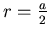 into the expression
for Ir gives for the moments of inertia about the
center of the sphere
into the expression
for Ir gives for the moments of inertia about the
center of the sphere
c:
We have
Return to title page.


Next: About this document ...
Birger Bergersen
2000-02-20