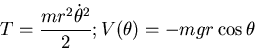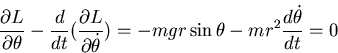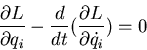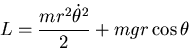

Next: About this document ...
15. Lagrangian dynamics
LAST TIMES
- We isolated a generic class of variational
problems.
- The goal was to find
a function z(x) for which the integral
over
some property
L(z,dz/dx,x) had an extremum.
- We derived the Euler-Lagrange equation
for the solution to the problem.
- We analyzed, as an example, the brachistochrone problem.
PRINCIPLE OF LEAST ACTION
(or Hamilton's principle)
We now reformulate mechanics by requiring
that every mechanical system is characterized by a Lagrangian
which is a function of the coordinates and velocities of
the particles constituting the system. The actual
trajectories are then those that minimize the
action
subject to boundary conditions at the endpoints. The integration
is with respect to time.
Logically we consider this to be a postulate replacing
Newton's laws as the foundation of mechanics. It remains
to construct the Lagrangian -something which, of course,
depends on the problem at hand. Also, we are not saying that
Newton was wrong- we want the Lagrangian formulation to reproduce
Newton's law when applicable.
Caveat: I mention in passing that the actual path
is not always a minimum for the entire path, but only for sufficiently
short segments. This is of no problem in practice.
In deriving the equation of motion we only use the extremum condition.
The Euler-Lagrange e equation is linear in the Lagrangian. We can multiply
L by a constant
without changing the equation of motion. We choose the Lagrangian
to have dimension of energy.
Example:
Particle in one dimension subject to
velocity independent force:
We put v=dx/dt. If the Lagrangian is
L=L(x,v,t)
the equation of motion is
We write
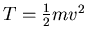 for the kinetic energy
for the kinetic energy
where a is the acceleration. Similarly if V(x) is the
potential energy
If we put L=T-V we see that equation of motion becomes
the familiar
f=ma
GENERALIZED COORDINATES
In our previous example x was the Cartesian coordinate of the particle.
It need not be, any coordinate that suffices to describe all
possible configurations of the system will do.
Example: THE PENDULUM
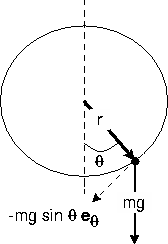
Instead of using the Cartesian coordinates of the mass
it is convenient describe the motion by the
angle 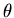 .
We used to call the length of the pendulum L. To
avoid confusion with the Lagrangian we rename it r.
.
We used to call the length of the pendulum L. To
avoid confusion with the Lagrangian we rename it r.
The kinetic and potential energies are
With L=T-V the equation of motion becomes
giving the expected result
The constraint on the motion
r2=x2+y2=const.
depends on the coordinates only (not on the velocities).
Such constraint are called holonomic. In both Lagrangian
and Newtonian mechanics such constraints can be handled by
simple substitution.
MANY DEGREES OF FREEDOM
Most often we are dealing with systems requiring a number
of generalized coordinates to describe the motion.
Suppose
N coordinates are required to specify the motion
(after we have substituted for the holonomic constraints).
We say that the system has N degrees of freedom.
The variational principle is now
We can carry out the variation independently for each of
the coordinates and obtain a set of N
Euler-Lagrange equations
i.e. one equation for each coordinate.
Example
PENDULUM WITH MOVABLE SUPPORT
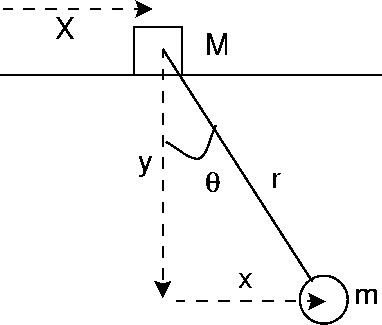
A pendulum of length r, mass m. Its support
has mass M and it can slide without friction horizontally (coordinate X). The horizontal and vertical
components of the pendulum mass are
The velocity components are
Hence the Lagrangian
is
L=T-V
We will come back to the equations of motion for this system later
GENERALIZED FORCES AND MOMENTA.
When the
kinetic energy is on the form
and V(x) is velocity independent, the equation of motion
can be written
where p is the momentum and f the force
In the general case:
-
-
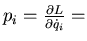 generalized momentum
generalized momentum
-
-
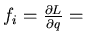 generalized force
generalized force
The Lagrangian equations of motion can thus be written:
If the Lagrangian does not depend explicitly on one of
the coordinates the corresponding generalized force is zero
and the corresponding generalized momentum is
conserved!
Example THE PENDULUM
The generalized force is
Physically the generalized force associated with the angle 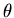 is the torque!
is the torque!
The generalized momentum is
which we recognize as the angular momentum. The
Lagrangian equation of motion is thus just
Rate of change of angular momentum=torque
Example
PENDULUM WITH MOVABLE SUPPORT
L=T-V
This Lagrangian doesn't depend explicitly on X hence
is conserved. A bit of reflection will convince you
that this is just the equation for the conservation
of linear momentum in the x-direction.
So there is nothing new!
We could have obtained the above results without resorting
to Lagrangians.
However, if the system is complicated the Lagrangian approach offers
the possibility of proceeding in a systematic fashion.
The systematic approach makes it much easier to avoid errors!.
SUMMARY
We have
- developed Lagrangian dynamics from the principle of
least action
- shown that for a conservative system with velocity-independent forces we could
reproduce Newtonian dynamics if we put for the
Lagrangian
L=T-V
- introduced generalized
- coordinates
- momenta
- forces
- shown that if Lagrangian did not
depend on a generalized coordinate the corresponding momentum
was conserved.
Return to title page.


Next: About this document ...
Birger Bergersen
1999-02-21