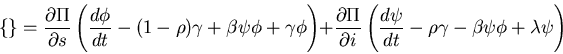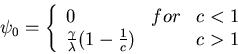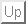

Next: About this document ...
5. Several variables, SIR-model
LAST TIME
- Gave examples Fokker Planck equation of type
- A-term drift term.
- B-term represented diffusion.
- Fokker-Planck equation linear if A depends on x
linearly and B is independent on x.
- Kramers equation demonstrated need to study case of more than one variable!
Today will discuss solution to linear multivariate problem.
GENERAL CASE:
Eliminate ci(t) term by transformation
yi=xi-ui(t)
Let ui be solution to
If Aij independent of t solution can be found
by elementary methods.
In general case may need to use approximate method!
ui(t) solution to macroscopic equation!
Find
Mean
satisfies
On matrix form
If at
the solution can
be expressed in terms of evolution matrix Y
where
Second moments
Covariance matrix
satisfies same equation as second moment.
On matrix form
With boundary condition
solution is
Can use this result to solve Focker-Planck equation
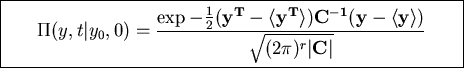
obtained by method of inspired guess.
Example from epidemiology
STOCHASTIC SIR MODEL
- Divide population into:
- susceptibles S
- infecteds I
- immune (removed) R
- New susceptibles are introduced at the rate
- New infecteds are introduced at a rate
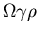 .
Interested in limit
.
Interested in limit
- The susceptibles are infected and become
infectious at the rate
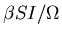 .
.
- The susceptibles die at the rate
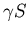 .
.
- The infected individuals are removed at the rate
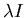 by death or
immunity.
by death or
immunity.
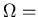 system size parameter.
system size parameter.
Master equation
Where
Raising and lowering operators
Express master equation in terms of raising and
lowering operators
OMEGA-EXPANSION
Expect that 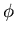 and
and 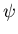 satisfy deterministic
rate equations and that s and i fluctuate and
satisfy a Fokker Planck equation.
satisfy deterministic
rate equations and that s and i fluctuate and
satisfy a Fokker Planck equation.
P(S,I,t) probability that S susceptibles and I
infecteds are present at time t.
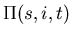 probability distribution for s,i.
probability distribution for s,i.
Factor 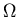 arising from normalization condition
arising from normalization condition
We have
Next, expand
| ES-1 |
= |
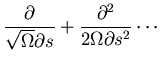 |
|
| ES-1-1 |
= |
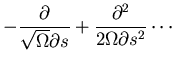 |
|
| EI-1 |
= |
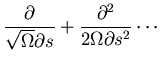 |
|
| EI-1-1 |
= |
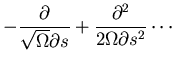 |
|
| ESEI-1-1 |
= |
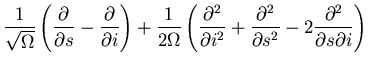 |
|
Substitution and solving for
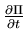 yields an expression of the form
yields an expression of the form
Term
must vanish:
Get rate equations
The Fokker Planck equation is then
where solution to rate equation is substituted for 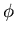 and
and 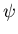 .
.
MACROSCOPIC STEADY STATE
Put time derivatives to zero
The steady state solutions satisfy
The positive solution is stable
where
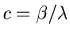 .
If
.
If 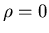 the expressions simplify to
the expressions simplify to
We plot below
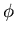 and
and
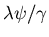 for
for
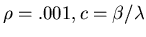 .
.
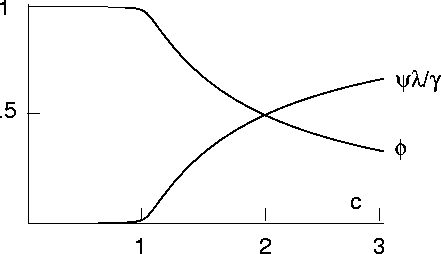
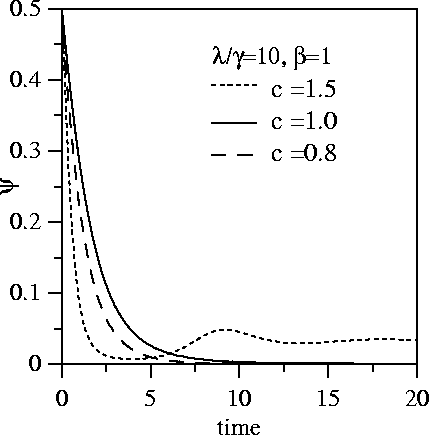
When c<1 (intermittent regime) only a very small number of individuals succumb to the disease
and an epidemic caused by immigration of an infectious individual
will quickly die out. The population will remain disease free until the next
infectious individual arrives. For c>1 the disease takes hold and
there will be a finite fraction of infectious individuals in the population
at all times (endemic regime).
VALIDITY OF EXPANSION
must require
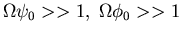 .
.
First condition hardest to satisfy.
- If
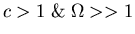 can put
can put 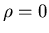 .
.
- if
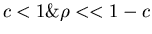 must have
must have
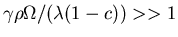 .
.
- if c=1 must have
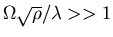 .
.
Interprete
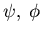 as ensemble average
of many realizations.
When macroscopic equations stable get
Gaussian fluctuations
as ensemble average
of many realizations.
When macroscopic equations stable get
Gaussian fluctuations
Damped oscillation in decay of fluctuation
due to drift in phase.
Can show no finite-size corrections
to order
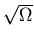 .
.
APPROACH OF MACROSCOPIC VARIABLE TO STEADY STATE
Initially half of population infected 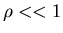
SUMMARY
- Can solve linear multivariate Focker-Planck equation
when macroscopic equation can be solved.
- When macroscopic equations stable, fluctuations Gaussian.
- Boundedness of fluctuation provides criterion for validity
of macroscopic treatemnt, in limit of large system size.
- Example SIR model from epidemiology.
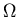 exansion works when infection endemic.
exansion works when infection endemic.
Click here for Return to title page
Click here for 6. Absorbing boundaries


Next: About this document ...
Birger Bergersen
1998-10-03
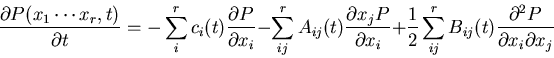
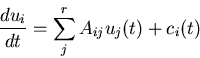
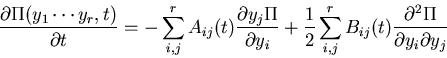
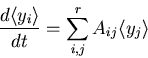
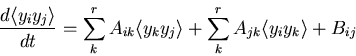
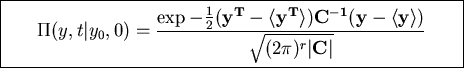
![\begin{displaymath}\frac{\partial P(S,I,t)}{\partial t}=
\sum_{S,I}[W(S,I\vert S',I')P(S',I',t)-W(S',I'\vert S,I)P(S,I,t)]\end{displaymath}](img27.gif)
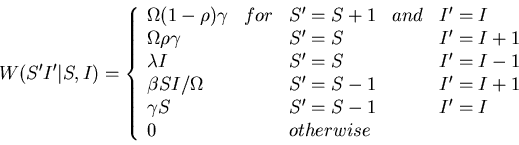
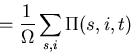
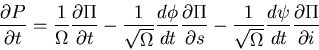
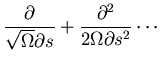
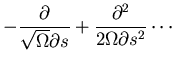
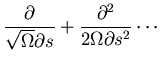
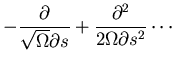
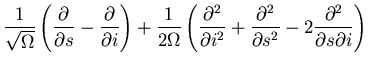
![\begin{displaymath}\frac{\partial\Pi}{\partial t}=\sqrt{\Omega}\{\}+[]+O[\frac{1}{\sqrt{\Omega}}]\end{displaymath}](img45.gif)