

Next: Two sub-recoil cooling methods
Up: No Title
Previous: No Title
Need three ingredients to understand Doppler cooling:
1. Three elementary processes of atom-light interaction:
2. Momentum conservation
v typically a few cm/s
3. Doppler shift
Construct velocity-dependent dissipative force on atom with two red detuned laser beams:
Red detuned
 absorption preferentially from laser beam opposing velocity (Doppler shift towards resonance)
absorption preferentially from laser beam opposing velocity (Doppler shift towards resonance)
 slows atom down towards v=0 if de-excitation mainly due to isotropic spontaneous emission (low intensity limit)
(
slows atom down towards v=0 if de-excitation mainly due to isotropic spontaneous emission (low intensity limit)
(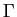 =natural line width)
=natural line width)
Force
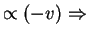 energy dissipation
energy dissipation
Ultimate limit for Doppler cooling
Atom cannot be cooled to v=0 because of random recoil from spontaneous emission (random walk in momentum space with increments 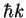 )
)
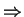 heating rate associated with recoil
heating rate associated with recoil
Landmark energy: Recoil energy
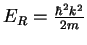
ER corresponds to temperature
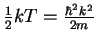 (
(
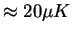 for Na)
for Na)
Note: Omitted discussion of so-called Sub-doppler cooling


Next: Two sub-recoil cooling methods
Up: No Title
Previous: No Title
Birger Bergersen
1998-12-12
![\includegraphics[height=3.5cm,width=14cm,angle=0]{elprocess.eps}](img1.gif)
![\includegraphics[height=3.5cm,width=14cm,angle=0]{elprocess.eps}](img1.gif)
![\includegraphics[height=1.5cm,width=10cm,angle=0]{momcons.eps}](img2.gif)
![\includegraphics[height=1.5cm,width=10cm,angle=0]{dopplersh.eps}](img3.gif)
![\includegraphics[height=10cm,width=3cm,angle=-90]{cool.eps}](img5.gif)
![\includegraphics[height=12cm,width=6cm,angle=90]{force.ps}](img7.gif)