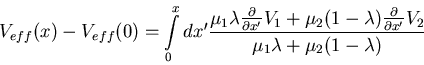

Next: About this document ...
Rolf Luchsinger Oct. 98
10. Molecular Motors
Experimental facts:
- nano-microscale
(
 thermal noise relevant)
thermal noise relevant)
- motors move along linear, periodic structure
(Kinesin and Dynein on Microtubule)
(Myosin on Actin)
- energy (ATP) is needed
- two states (bound
 unbound)
unbound)
- isothermal (
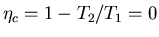 )
)
FORCED THERMAL RACHET
(Magnasco,1993)
LANGEVIN Eq. for an over damped particle
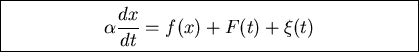
where
f(x) = f(x+l)
Corresponding FOKKER-PLANCK Eq.
(Smoluchoswki equation)
with
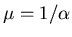 (mobility)
(mobility)
Rewrite the Smoluchowski Eq.
Stationary solution:
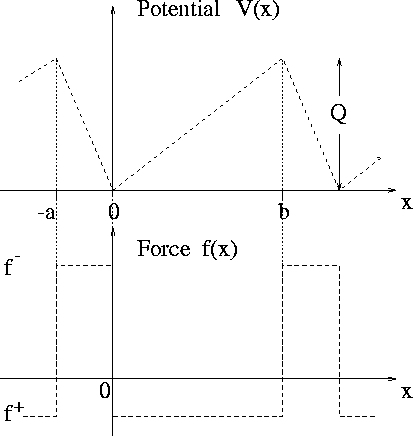
Simplest case: Piecewise linear potential:
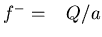
f+ = -Q/b
1)
P(-0) = P(0) (continuous)
2)
P(-a) = P(b) (periodic)
3)
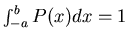 (normalized)
(normalized)
Investigate different cases:
a.) F = 0:
b.)
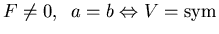 :
:
c.)
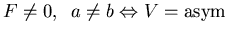 :
:
where
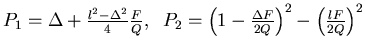
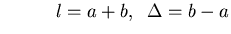
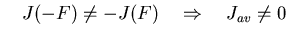
The average probability current Jav as a function
of the magnitude of the external forcing.
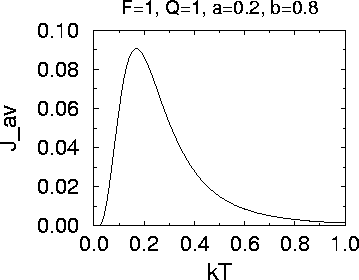
The average probability current Jav as a function
of the temperature.
A net probability current Jav results for:
- Asymmetric Potential
- Finite Temperature
- Forcing with time correlations
There are physical applications of the Forced Thermal Ratchet
(Molecular Pumps, Filters) but the relevance for biological molecular
motors is not clear.
TWO-STATE MODEL
(Prost et al, 1994)
Instead of the time-correlated forcing, this model assumes a two-state
system (bound/unbound) for the motor. The external action (ATP hydrolysis)
drives the transition rates between the two states away from their
equilibrium values.
This set of equations can be transformed to an equation for the
total probability current J=J1+J2 as a function of P=P1+P2
If the effective force
Feff = (Veff(x+l)-Veff(x))/l
vanishes, then J vanishes.
One can show that
- V1, V2 symmetric
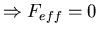
-
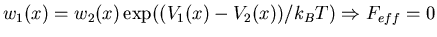 (detailed balance)
(detailed balance)
- detailed balance broken by energy input
through ATP
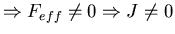
An effective force can be obtained by breaking detailed balance.
The basic mechanism for the Two-State System can be understood
from the Figure. A particle makes a transition from 1 to 2. It diffuses
in state 2. After a certain time there is a finite probability that
it will fall into the next well during the transition from 2 to 1.
Matching of transition rates, diffusion rate and potential form
is important.
SUMMARY
- Basic understanding of molecular motors
emerges
- Theories based on Fokker-Planck equations
- Three important ingredients:
-broken symmetry
-noise
-correlated forcing/broken detailed balance
- Stochastic resonance behavior
- So far the importance of noise in biological motors not proven,
but if models are correct, then:
Noise keeps us going!
REFERENCES:
M.O. Magnasco, Phys.Rev.Lett. 71, 1477 (93)
J. Prost et al, Phys.Rev.Lett. 72, 2652 (94)
F. Jülicher et al, Rev.Mod.Phys. 69, 1269 (97)
R.D. Astumian, Science 276, 917 (97)
Click here for Return to title page
Click here for 11. Lévy-stable distributions


Next: About this document ...
Birger Bergersen
1998-10-14
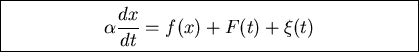
![\begin{displaymath}\frac{\partial P(x,t)}{\partial t}= \mu \left[-\frac{\partial...
...f(x)+F(t)\Bigg)
P+ k_B T \frac{\partial}{\partial x} P \right]\end{displaymath}](img8.gif)
![\begin{displaymath}J(x,t) =
\mu \left[- k_B T \frac{\partial}{\partial x}P +\Bigg(f(x)+F(t)\Bigg)P\right]\end{displaymath}](img11.gif)
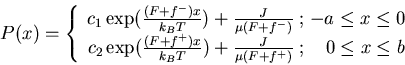
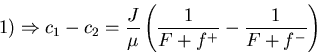
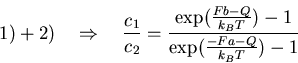
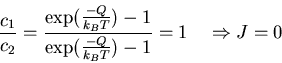
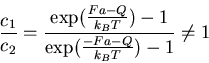
![\begin{displaymath}J(F) = \frac{P_2^2 \sinh(lF/2k_B T)}{k_B T (l/Q)^2
\{\cosh[...
...F/2)/k_B T]-\cosh(lF/2k_B T)\}
-(l/Q)P_1P_2\sinh(lF/2k_B T)} \end{displaymath}](img26.gif)
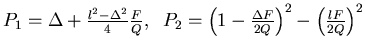
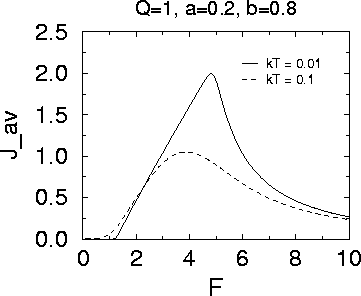
![\begin{displaymath}J_i =
\mu_i \left[- k_B T \frac{\partial}{\partial x}P_i - P_i\frac{\partial}{\partial x} V_i
\right]\end{displaymath}](img34.gif)
![\begin{displaymath}J =
\mu_{eff} \left[- k_B T \frac{\partial}{\partial x}P - P\frac{\partial}{\partial x} V_{eff}
\right]\end{displaymath}](img35.gif)