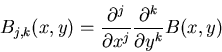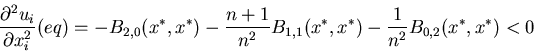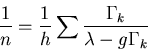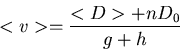

Next: About this document ...
Stochastic Dynamics in Game Theory:
comments on some papers by Matteo Marsili and Yi-Cheng Zhang
Margarita Ifti
- Starting point: a theory for economic equilibria. Game Theory.
- Dealing with economics, not with finance. Finance is a dynamical system
out of equilibrium, where players speculate on future market's fluctuations.
- Rational behaviour, but deviations from rationality are present.
Infinite precision is impossible, if not at infinite cost.
- Similarity with Stat Mech: minimalization of energy-maximization of
utility, Nash equilibria-ground states, deviations from
rationality-temperature. Leads to a natural definition of stochastic
dynamics in Game Theory.
- Use Langevin approach: fluctuations around Nash equilibria in specific
games with a large number of players.
Each of the n players can control a continuous variable or "strategy"
xi. His utility function ui depends on his own strategy as well as on
others'. Each player continuously adjusts his variable in order to
maximize his utility. He also faces stochastic shocks and so his variable
becomes a continuous time stochastic process.
Analogy with Statistical Mechanics:
- negative utility plays the role of an energy;
- stochastic force on a player like that arising from a heat bath;
- effects of fluctuations similar to effects of entropy;
Main difference:
- In Stat Mech each degree of freedom evolves to minimize a global
variable (energy), in Game Theory each degree of freedom maximizes its
own (partial) utility.
We focus on a particular class of games with global interaction.
Nash equilibria are stationary points of the dynamics. Two main
equilibria exist: i) non-competitive equilibria, where each player's
equilibrium strategy is determined by its interactions with the rules of
the game, and ii) competitive equilibria, which result from the
aggressive competition of each player with all the others.
Game Theory and Evolution
Large number of interacting agents. Each agent has a spectrum of
strategies and a utility or payoff function, which depends on the
strategy. Game Theory assumes that payoff functions are common knowledge
and that each player behaves rationally. Stable states of the system are
called Nash Equilibria. A strategy xi* is a NE if each player's
utility for fixed opponents' strategies, is a maximum for xi=xi*. The
NE strategies are then such that no player has incentives to change them,
since any change would result in utility loss. Nash showed that each game
has at least one such equilibrium.
Cournot Game and Tragedy of the Commons
2 firms produce quantities x1 and x2 of a product
Price depends on total quantity produced: P(X)=a-bX
Cost is proportional to x: C=cxi
Payoff function then:
ui=xi[P(x1+x2)-c]=xi[a-c-b(x1+x2)]
Best response is obtained by maximizing
u1(x1,x2) w.r.t. x1
for fixed x2.
Leads to
 .
.
For n firms,
 with payoff
with payoff
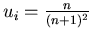
Known as the Tragedy of the Commons: the common resource is almost
depleted, and the payoff per player is very small.
Repeated Games and Evolutionary Game Theory
A strategy describes the action each player has to do at each stage.
Also, the single stage utility is replaced by a utility which accounts
for many stages, usually a discount factor (i.e. an exponential weight
function for future utility).
- Replicator dynamics model: in its simplest form, it assumes that the
individuals playing a given strategy reproduce at a rate proportional to
their utility. Its applications have been limited to two player games,
generalisation is very complex. Rationality is not assumed: players keep
playing the game the way their ancestors did. Rational NE results from the
selective evolution of replicator dynamics.
A simple realistic dynamics with almost rational players is
studied.
Langevin dynamics:
Langevin equation:
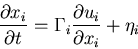 |
(1) |
where the stochastic term models deviation from perfect rationality.
The first part (deterministic) assumes "local rationality": each agent
knows in which direction his utility increases, i.e. they know ui in a
small neighbourhood of xi. Weakens perfect rationality assumption.
The stochastic term has a part that represents the individual "problems"
(e.g. illness) and the global ones (e.g. earthquake). Hence the
correlation of the stochastic terms is taken:
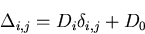 |
(2) |
The Langevin approach includes "thermal" fluctuations, allowing to
analyse the stability of NE. Also, it gives a "free energy" measure,
which enables us to distinguish the real "ground state" from "metastable"
states. Curiously, in an ideally slow cooling down only the state with the
smallest "free energy" is selected, independently of the initial
conditions! (in the evolutionary approach the final state is uniquely
determined by the initial conditions).
The Model
Always focusing on global interactions, consider situations where the
payoff function for player i is:
ui(xi,x-i)=-B(xi,<x>) with

Because of the symmetry of the interaction, the NE are symmetric:
xi* =
x* for all i, and x* satisfies the equation
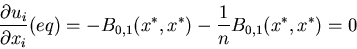 |
(3) |
where for convenience we have defined
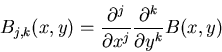 |
(4) |
and
B0,0(x,y)=B(x,y).
Also, a NE must be a maximum w.r.t xi, i.e.
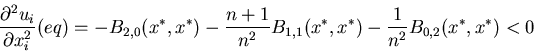 |
(5) |
We can always choose x*=0 (if not, a linear transformation will do).
Also choose B(0,0)=0. Expanding the deterministic part to the leading
order, we arrive to the equation:
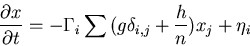 |
(6) |
where
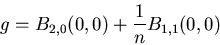 |
(7) |
and
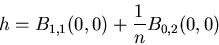 |
(8) |
Stability requires that all the eigenvalues of the matrix
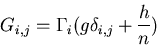 |
(9) |
be positive. These are given by the equation:
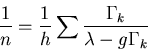 |
(10) |
But if g > 0, and h + g > 0, all the eigenvalues are positive.
The equation above is a multivariate Ornstein-Uhlenbeck process.
Fluctuations around the NE are described by the matrix of correlations.
The correlation functions decay exponentially, with correlation time given
by the minimum eigenvalue.
After some algebra, we find that the average utility is:
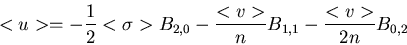 |
(11) |
with
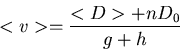 |
(12) |
The last term is the average utility at the NE in presence of
fluctuations. This would be the utility of a player who maintains the NE
strategy xi=0 even in presence of fluctuations. It is interesting to
note that it is possible to get an average utility larger than those
for NE strategy. Loosely speaking, it means that in a game with random
deviations from rationality, player who are affected by the randomness may
happen to receive a higher payoff (in average) than those who behave
rationally (xi=0). It pays to be stupid sometimes! The
condition for this to happen is
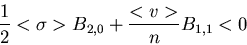 |
(13) |
As expected, the fluctuations grow with Di and D0. There are three
qualitatively different cases, as shown in figure 2:
a) when B2,0, B1,1 and B0,2 are all finite and positive. We
have a normal behaviour with small fluctuations. Fluctuations increase the
average utility and a rational behaviour is generally more rewarding.
b)
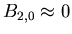 ,
B1,1 and B0,2 are finite and positive.
Then g is small and the fluctuations are proportional to n. Generally
B2,0 = 0 is typical of competitive equilibria. Indeed it means that
each player does not feel the effects of change in their xi directly.
Rather they are transmitted through the change on the global variable
<x>. Large fluctuations come together with large relaxation times.
Finally, the average utility is decreased.
c)
,
B1,1 and B0,2 are finite and positive.
Then g is small and the fluctuations are proportional to n. Generally
B2,0 = 0 is typical of competitive equilibria. Indeed it means that
each player does not feel the effects of change in their xi directly.
Rather they are transmitted through the change on the global variable
<x>. Large fluctuations come together with large relaxation times.
Finally, the average utility is decreased.
c)
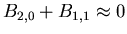 . Also in this case large fluctuations
occur, since
g + h << 1. The smallest eigenvalue is small, and this
means large correlation time. Only one eigenvalue is small in this case,
unlike case b). Also, xi fluctuate in phase, thus yielding a large
fluctuation of their sum. Finally, the fluctuations may decrease the
average utility in this case. Furthermore, a player who behaves
rationally receives a smaller payoff for sure!
Expansion to higher order shows that the fluctuations experienced by a
player are smaller the faster his dynamics (acceptable intuitively).
. Also in this case large fluctuations
occur, since
g + h << 1. The smallest eigenvalue is small, and this
means large correlation time. Only one eigenvalue is small in this case,
unlike case b). Also, xi fluctuate in phase, thus yielding a large
fluctuation of their sum. Finally, the fluctuations may decrease the
average utility in this case. Furthermore, a player who behaves
rationally receives a smaller payoff for sure!
Expansion to higher order shows that the fluctuations experienced by a
player are smaller the faster his dynamics (acceptable intuitively).
Conclusions
- Competitive Nash equilibria are usually affected by very large
fluctuations, which increase with the number of players. Competition
leads to broad distributions and large inequalities in an economic
system. This is reminiscent of Pareto Law of distribution of incomes.
Inequalities increase with the number of players.
- Competitive equilibria are also characterized by large relaxation
times, which are proportional to n, and by a negative correlation between
players' strategies. This means that two players tend to have opposite
fluctuations around Nash Equilibrium.
- At odd with Stat Mech, where fluctuations always increase the energy of
the system, in a game theoretical system, under particular conditions,
fluctuations increase the utility (i.e. decrease the energy).
- Fluctuations, in general displace NE, and in some cases, for strong
randomness, a NE can disappear.
Return to title page.


Next: About this document ...
Birger Bergersen
1998-12-21