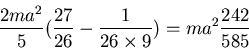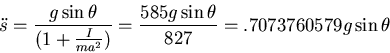

Next: About this document ...
PHYSICS 206
Problem set 8 2001. Solution.
Problem 1:
Perhaps the most direct method to solve this problem is to start from the expression for the angular moment for a sum of mass points dm
Consider a mass element dm=mds/a a distance s from the center of mass of the rod. The z-axis is the axis of rotation. At some instance
the mass element will be located at
The corresponding velocities are
a:
The angular momentum is
b:
The torque is
Problem 2:
a:
b:
The volume of the ball excluding the cavity is
If the higher density ball had been solid its mass would have been
27m/26. The moment of inertia is thus
Problem 3:
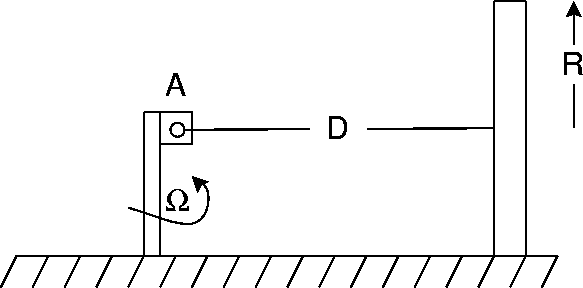
We let A be the origin of our body centered coordinate system,
1 the direction out of the plane of the paper, 2 the axis from A to the center of the wheel and 3 the vertical. For the wheel to stay on its path (without falling or flying up)
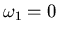 .
From Euler's equations
.
From Euler's equations
We have
For the wheel to roll without slipping
The moment of inertia of a disk about an axis perpendicular to the plane of the disk
is
The moment of inertia of a disk about an axis in the plane of
the disk through its center is mR2/4 giving
Hence the torque is
where n is the normal force. We find
Return to title page


Next: About this document ...
Birger Bergersen
2001-04-08
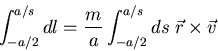
![\begin{displaymath}\vec{N}=\frac{d\vec{l}}{dt}=\frac{ma^2\omega^2}{12}\cos\theta\sin\theta[
\hat{i}\sin(\omega t)-\hat{j}\cos(\omega t)]\end{displaymath}](img6.gif)