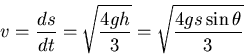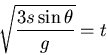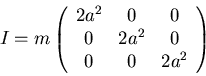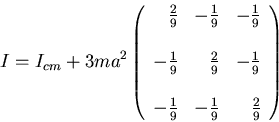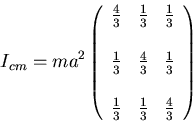

Next: About this document ...
Large PHYSICS 206
Problem set 7 2001. Solution.
Problem 1:
a:
The velocity of the point of contact is zero. Therefore, the force of friction does no work and energy is conserved.
Let h be the vertical drop, v the velocity of the center of mass, and 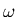 the angular velocity, and
the angular velocity, and
the moment of inertia. Energy conservation gives
where we have used 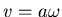 .
If s is the distance travelled we obtain
.
If s is the distance travelled we obtain
which can be integrated to give
or
b:
We have for the torque with f the force of friction
c:
The normal force is
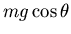 ,
so the the maximum angle is given by
,
so the the maximum angle is given by
Problem 2:
a:
The moment of inertia tensor about the origin is
b: The center of mass is at
c:
We have from the parallel axis thorem
giving
For reasons of symmetry one of the pricipal axis must extend in the direction from the origin to
the center of mass
The corresponding moment of inertia is
I3=2ma2
Any axis perpendicular to this axis is also a principal axis (the object is a symmetric top)
I2=I1=ma2
A possible choice of directions is
Problem 3:
a:
The kinetic energy is
The angular velocity is determined by the condition that the point of contact
has zero velocity
The moment of inertia of a sphere is I=2ma2/5 so that
b:
Return to title page.


Next: About this document ...
Birger Bergersen
2001-04-02